Transformace je popsána funkcí ![]() , která váže souřadnice
, která váže souřadnice
![]() v původním obrázku a souřadnice
v původním obrázku a souřadnice
![]() v novém obrázku:
v novém obrázku:
| (1) |
Obrazovou funkci původního obrázku již máme značenou ![]() . Označíme-li
obrazovou funkci nového obrázku
. Označíme-li
obrazovou funkci nového obrázku ![]() , pak platí:
, pak platí:
| (2) | |||
| (3) |
Tyto vztahy můžeme přepsat do kompaktnějšího tvaru:
kde ![]() ,
, ![]() a
a ![]() jsou řádky matice
jsou řádky matice
![]() tvořené koeficienty ze vztahů (4) a (5):
tvořené koeficienty ze vztahů (4) a (5):
![\begin{displaymath}
{\bf A}=\left[\begin{array}{c}{\bf A}_1\\ {\bf A}_2\\ {\bf ...
... a_{22} & a_{23}\\ a_{31} & a_{32} & a_{33}\end{array}\right]
\end{displaymath}](img22.png) |
(7) |
V této části si ukážeme, jak vypočítat matici ![]() , která
reprezentuje projektivní transformaci mezi dvěma obrazy. V těchto dvou
obrazech mějme tzv. lícovací body, tj. body které si v obrazech vzájemně
korespondují (označeny červeným křížkem):
, která
reprezentuje projektivní transformaci mezi dvěma obrazy. V těchto dvou
obrazech mějme tzv. lícovací body, tj. body které si v obrazech vzájemně
korespondují (označeny červeným křížkem):
![\includegraphics[width=5cm]{figures/let1s.ps}](img23.png) |
![\includegraphics[width=7.5cm]{figures/let2s.ps}](img24.png) |
Lícovacích dvojic nech<< je ![]() . Pro každou dvojici lícovacích bodů
. Pro každou dvojici lícovacích bodů
![]() mají platit vztahy (6), kam za
mají platit vztahy (6), kam za ![]() dosadíme
dosadíme ![]() a za
a za ![]() dosadíme
dosadíme ![]() . Pak hledáme
matici
. Pak hledáme
matici ![]() takovou, aby (6) byla splněna pro všechny lícovací
dvojice.
takovou, aby (6) byla splněna pro všechny lícovací
dvojice.
Nalezení ![]() je obzvláště jednoduché, nebo<< vztahy (6) jsou v
prvcích
je obzvláště jednoduché, nebo<< vztahy (6) jsou v
prvcích ![]() lineární. Úpravou vztahů totiž dostaneme:
lineární. Úpravou vztahů totiž dostaneme:
Utvoříme z prvků matice ![]() vektor
vektor
![]() a zapíšeme lineární soustavu rovnic pro tento vektor:
a zapíšeme lineární soustavu rovnic pro tento vektor:
Soustavu vyřešíme a tím dostaneme vektor ![]() , který pak jen
přeskládáme do matice
, který pak jen
přeskládáme do matice ![]() a tím jsme hotovi.
a tím jsme hotovi.
![${\bf U}^i=\left[\begin{array}{c}{\bf u}^i \\ 1\end{array}\right]$](img35.png) , a
když přeskládáte řádky, dá se soustava (10) napsat ve velice kompaktním tvaru:
, a
když přeskládáte řádky, dá se soustava (10) napsat ve velice kompaktním tvaru:
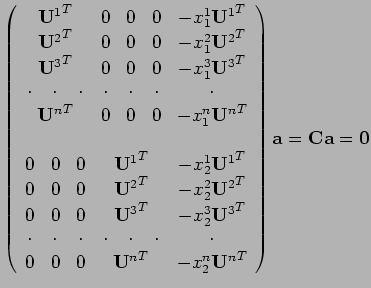 |
(11) |
V praxi se používá korespondencí více než 4, aby se zmenšil vliv chyby
při určení korespondujících bodů. Kvůli chybám je však také nulový
prostor matice [![]() ] prázdný a vektor [
] prázdný a vektor [![]() ] se hledá ve
smyslu nejmenších čtverců, tj. určí se jako
] se hledá ve
smyslu nejmenších čtverců, tj. určí se jako
| (12) |
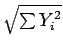 ).
).
Nalezení vektoru ![]() se v takovém případě udělá pomocí SVD
(Singular Value Decomposition). Lze použít následující MATLAB kód:
se v takovém případě udělá pomocí SVD
(Singular Value Decomposition). Lze použít následující MATLAB kód:
% vypocitej vektor a
[u,d,v]=svd(C);
a=v(:,end);
Při použití metody nejmenších čtverců se chyba "rovnoměrně rozdělí" do všech sloupců, někde představuje zanedbatelnou změnu, jinde změnu velmi výraznou. Tomu je možné zabránit normalizací. Body v každém souřadném systému zvlášť se transformují tak, aby jejich težiště bylo v počátku a průměrná vzdálenost od počátku byla rovna sqrt(2), pro výpočet normalizační transformace lze použít funkci Tu=normu(u). Homografii An vypočtenou na normalizovaných bodech je pak nutné převést zpět A = inv(Tx)*An*Tu.
