Pixel Based Image registration
You will be provided with
6 image pairs like the one shown in
figure 1. You are required to hand in a report and a Matlab program that takes
two images and registers them. The report should show the registered images and
the transformation parameters for all image pairs provided. The images may be
downloaded as a compressed RAR file here. You also MAY need couple of optimization toolbox functions fminunc.zip (depending on version of Matlab, in classroom (7.6) it is not necessary).
|
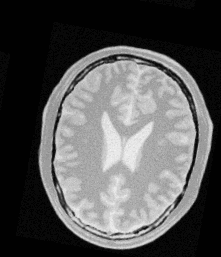
Proton Density Brain Image 1 |
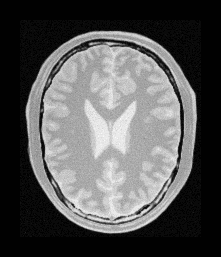
Proton Density Brain Image 2 |
|
|
|
Figure 1
Transformation
We assume that the
geometrical transformation we search for is a combination of rotations and
translations. This kind of transformation is called a rigid transformation and maps
a point of coordinates [x, y] to point [u,
v]. It may be written down as follows:
u =
x*cos( a ) + y*sin( a ) + x0;
v = - x*sin( a ) + y*cos( a ) + y0;
Where x0 is the x translation, y0 is the y translation and a is the
rotation angle. The rotation is around point [0,0].
This transformation may also
be expressed in matrix form using homogenous coordinates as
|
u |
|
cos( a ) |
sin( a ) |
x0 |
* |
x |
|
v |
= |
-sin( a ) |
cos( a ) |
y0 |
y |
|
|
1 |
|
0 |
0 |
1 |
1 |
SubTask 1
Implement function rigidTransformation that receives an image (img)
and 3 transformation parameters (angle, x displacement and y displacement) and
returns the image transformed by the parameters. Its syntaxes should be:
imgdef = rigidTransformation (a, xd, yd,img);
We recommended using the following functions provided by Matlab:
MaketForm
Maketform creates a geometric transformation structure.
tform= maketform( ‘affine’, A);
The structure will map
points [x y] to [u
v] by.
|
u |
|
([x
y 1 ] * A)T |
|
v |
= |
|
|
1 |
|
Note that for this
matrix A it is also true that:
|
u |
|
AT * |
x |
|
v |
= |
y |
|
|
1 |
|
1 |
Imtransform
Imtransform transforms an image according to a 2-D spatial transformation
returned by maketform.
imgdef= imtransform(double(img), tform,’Xdata’, [ 1 s1] , ‘Ydata’ , [1 s2]);
To insure that img
and imgdef are of the same size s1 = number of columns of
img and s2 = number of rows of img2.
Function imtransform will return an image of the same type as img. Make sure to that
the input and output images are in double format. If not the transformation
will not be precise enough for registration purposes.
Image Similarity Criteria
To compare the images we
will use a Sum of Square Differences
(SSD) criterion. The SSD is defined as:
![]()
Subtask 2
Write the following
function:
[ J ] = SSD(
X, img1, img2);
X is a vector containing the deformation parameters
(angle, x translation, y translation).
The first returned value, J, is the sum of square differences of img1
and img2 deformed by parameters X (use
the function rigidTransformation that you implemented in the previous point).
Subtask 3
For the image pair 1 the
correct parameters are [-10 37.2
-1.4]. Plot the dependence of the
criterion on the angle of the rotation in the vicinity of the correct solution.
Keep the translation parameters constant. Use the functions you implemented in the previous point.
Optimization
Optimizing a function of
several variables is a complex task. Matlab provides a series of functions to
solve this problem. We will use the function fminunc to find the
parameters that minimize the SSD between img1 and img2.
Fminunc
Function fmiunc
finds the minimum of a scalar function of several variables, starting at an
initial estimate. This is generally referred to as unconstrained nonlinear
optimization.
We will use the following
syntaxes to call it:
XF =fminunc (@(X) SSD(X, img1, img2), start, opt);
The first argument (@(X) SSD(X, double(img1), double(img2))) means that we shall optimize the array X of function SSD(X,
double(img1), double(img2)).IMPORTANT:
the images must be passed as double precision arrays to the optimizer . If you
don’t convert the images before passing the optimizer will not be precise
enough and will fail.
The second argument is the
initial search point (e.g. start=[0 0 0])
The third argument, opt is
an optimization options structure. We can initialize it like this
opt=optimset(‘LargeScale’,’off’,’Display’,’iter’);
LargeScale=off tells the function not to use a large-scale algorithm.
For our problem medium scale algorithms are more appropriate. Display= iter displays the output at each iteration, letting you see the progress of
the optimization.
The algorithm used when fminunc
is called like this is the BFGS Quasi-Newton method with a mixed quadratic and
cubic line search procedure. Gradients are estimated using finite differences.
Subtask 4
Register the first image
pair. Your result should be a vector with values nearly equal to [-10
37.2 -1.4]. First try a starting point relatively close to
this solution. Show the difference between the registered and unregistered
image pairs. If the results are correct they should look like those of figure
2.
|
Image Difference Before Registration |
Image Difference After Registration |
|
|
|
Figure 2
Apply
the function on all provided image pairs. Write down the time required for the
registration (check functions tic, toc or clock for this), the criterion
value achieved, the final parameters and number of iterations needed.
Evaluate
the behavior of the algorithm for different starting points.
Subtask 5
When
using imtransform you may specify the kind
of interpolation to be used (see Matlab help of imtransform). Change your
function and try using different kinds of interpolation ('bicubic', 'linear' and
'nearest' (=nearest neighbour) ) for starting point [0 0 0] with the example image pair and with some point closer to the solution. Does
it allways converge? Compare visually the image transformed with the same parameters but different interpolation methods. Explain the results and include in the report.