 Matched Filtering
Matched Filtering
 Correlation Analysis
Correlation Analysis
 Correlation Analysis
Contents
Global Contents
Correlation Analysis
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
Definition: The circular cross-correlation of two signals 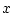 and
and
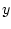 in
in  may be defined by
may be defined by
(Note that ` ' is an integer variable, not
the constant
' is an integer variable, not
the constant  .) The term ``cross-correlation'' comes from
statistics, and what we have defined here is more properly
called a ``sample cross-correlation.''
That is,
.) The term ``cross-correlation'' comes from
statistics, and what we have defined here is more properly
called a ``sample cross-correlation.''
That is,
 is an
estimator8.3 of the true
cross-correlation
is an
estimator8.3 of the true
cross-correlation  which is an assumed statistical property
of the signal itself. This definition of a sample cross-correlation is only valid for
stationary stochastic processes, e.g., ``steady noises'' that
sound unchanged over time. The statistics of a stationary stochastic
process are by definition time invariant, thereby allowing
time-averages to be used for estimating statistics such
as cross-correlations.
which is an assumed statistical property
of the signal itself. This definition of a sample cross-correlation is only valid for
stationary stochastic processes, e.g., ``steady noises'' that
sound unchanged over time. The statistics of a stationary stochastic
process are by definition time invariant, thereby allowing
time-averages to be used for estimating statistics such
as cross-correlations.
The DFT of the cross-correlation is called the cross-spectral
density, or ``cross-power spectrum,'' or even simply ``cross-spectrum'':
by the correlation theorem (§7.4.7).
Recall that the cross-correlation operator is cyclic (circular)
since  is interpreted modulo
is interpreted modulo  . In practice, we are normally
interested in estimating the acyclic cross-correlation
between two signals. For this (more realistic) case, we may define
instead the unbiased sample cross-correlation
. In practice, we are normally
interested in estimating the acyclic cross-correlation
between two signals. For this (more realistic) case, we may define
instead the unbiased sample cross-correlation
where we choose  (e.g.,
(e.g.,
 ) in order to have
enough lagged products at the highest lag that a reasonably accurate
average is obtained. The term ``unbiased'' refers to the fact that
the expected value8.4[28] of
) in order to have
enough lagged products at the highest lag that a reasonably accurate
average is obtained. The term ``unbiased'' refers to the fact that
the expected value8.4[28] of
 is the true
cross-correlation
is the true
cross-correlation  of
of 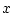 and
and 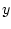 (assumed to be samples
from stationary stochastic processes).
(assumed to be samples
from stationary stochastic processes).
 Matched Filtering
Matched Filtering
 Correlation Analysis
Correlation Analysis
 Correlation Analysis
Contents
Global Contents
Correlation Analysis
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)
![]() and
and
![]() in
in ![]() may be defined by
may be defined by


![]() is interpreted modulo
is interpreted modulo ![]() . In practice, we are normally
interested in estimating the acyclic cross-correlation
between two signals. For this (more realistic) case, we may define
instead the unbiased sample cross-correlation
. In practice, we are normally
interested in estimating the acyclic cross-correlation
between two signals. For this (more realistic) case, we may define
instead the unbiased sample cross-correlation
