Aubrecht Emil, Kocián Jan                                                                                                         17.5.2000

 

PVI - úloha 2

Rekonstrukce scény

Úkoly

Pomocí MatLabu rekonstruujte scénu ze dvou obrázků objektu sejmutých kamerami, když mezi body je známá korespondence.

Potřebná data

dva vyhovující obrázky

Obecný postup

Řešení úlohy lze rozložit na následující části:

1.   Příprava dat

Pomocí modulu corrgui jsme ve dvou vstupních obrázcích vybrali několik (15) korespondujících bodů a jejich souřadnice uložili k dalšímu zpracování. Máme tedy obrazové body (u=( u_i, v_i, 1), u’=( u_i‘, v_i‘, 1)). (v obrázku vypadají takto: *****)

2.   Výpočet fundamentální matice Q

Fundamentální matice nám poskytuje korespondenci mezi oběma prostory: u^T.Q.u’=0. Po úpravách získáme rovnici ve tvaru A.q=0, kde A je matice nx9, q vektor 9x1 z matice Q (Q₁₁, Q₁₂, ...), ,
Pro řešení výsledné rovnice (soustavy) nám postačí zadání 8 bodů, pro a více bodů je již soustava přeurčená. Pro 8 bodů lze tedy vyřešit zadanou soustavu, pro větší počet bodů je nutno použít přibližnou metodu výpočtu, která nám nalezne matici “co nejbližší“ matici k matici A s hodností 8 - například Singular Value Decomposition (SVD).
V praxi se nám osvědčilo k výpočtu použít co nejvíce bodů (všechny).

3.   Výpočet epipolár l, l‘ a epipólů e, e’

Epipoláry určíme pomocí fundamentální matice Q a souřadnic naklikaných (obrazových) bodů: l=Q.u’, l‘=u^T.Q. Získané epipoláry zobrazíme jako úsečky do zdrojových obrázků (jeden bod zvolíme druhý na základě l resp l‘ dopočítáme) (v obrázku: -----).
Homogenní souřadnice epipólů e, e’ nalezneme ve třetích sloupcích matic U, V, získaných SVD fundamentální matice Q ([U.S.V] = svd(Q))(v obrázku: *****).

4.   Rekonstrukce geometrie skutečné scény ze zadaných P, P’

Použity jsou předem známé projekce kamer P, P’ ze souboru pointcal_mat.mat. Víme, že obrazový a reálný prostor jsou svázány projekčními maticemi: a.u=PX, a’.u’=P’X, kde X jsou souřadnice rekonstruované scény a a, a’ nějaká nenulová reálná čísla.
Označíme P=(A | b) a P‘=(A‘ | b‘), kde matice A, A’ mají velikost 3x3 a sloupcový vektor b, b’ 3x1. Hledané X’, X’’ získáme jako řešení následujících rovnic: (nejprve určíme a, a’ a poté zpětným dosazením X’, X’’)

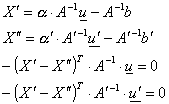
Výsledné souřadnice skutečné scény X vypočítáme jako průměr X’, X’’ a zobrazíme ve 3D (v obrázku: ****).
V praxi se průměrování (které nemá fyzikální opodstatnění) patrně projeví na chybě při rekonstrukci!

Nyní provedeme zpětnou projekci skutečných bodů do obrazu, tedy newu=P.X, newu’=P’X, po normalizaci zobrazíme (v obrázku: ****)

5.   Výpočet vlastních projekčních matic myP, myP’ a rekonstrukce scény pomocí nich
Provedeme volbu: myP=(I(3,3) | O(3,1)), kde I je jednotková matice a O je nulová matice. Druhá projekční matice má tvar: myP’=(A | b), kde matice A=(a₁, a₂, a₃) má velikost 3x3 a b je sloupcový vektor 3x1 (jedná se o jiné proměnné než v bodě 4!), b má hodnotu b=e’.
Z rovnosti Q.A=-A^T.Q^T (Q.A je antisymetrická matice) dostáváme 6  rovnic o 9 neznámých: W.a=0, matice W (6x9), koeficienty f1, f2, f3 jsou řádky fundamentální matice Q:

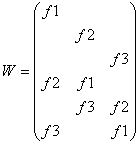
Provedením SVD matice W ([U D V] = svd(W)), se v 6 až 9 sloupci vzniklé matice V nalézají a¹ a², a³, a⁴, (báze jádra W). Naše hledané a je jejich lineární kombinací (s koeficienty a₁, a₂, a₃, a₄). Nyní se pokusíme najít takovou kombinaci a₁, a₂, a₃, a₄, aby požadovaná matice A bylo co nejvíce regulární (zjistíme opět pomocí SVD, kdy ve vzniklé matici D, chceme maximalizovat poměr posledního prvku na diagonále ku prvnímu). Z matice A a sloupcového vektoru b sestavíme myP’.

Analogicky s bodem 4 pomocí nových projekčních matic myP, myP’ vypočteme souřadnice v (projektivně) rekonstruované scéně myX (ty ovšem nemá smysl zobrazovat) a opět provedeme zpětnou projekci do obrazu a zobrazíme (v obrázku: oooo).

6.   Výpočet transformační matice H
Transformační matice H (4x4) nám svazuje souřadnice (projektivně) rekonstruované scény (myX_i) se souřadnicemi skutečné scény (X_i): m_i.myX_i=H.X _i. Po dosazení myX_i^T=(x_i y_i z_i w_i), X_i^T=(), m_i  jsou reálná čísla, a přepisu soustavy dostáváme:

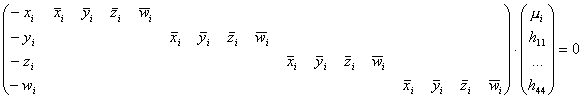
velká matice Z je pro 5 bodů velikosti 20x21. Vyřešením soustavy pro naše body (opět využijeme též SVD) získáme požadované H.
V praxi byl patrný vliv počtu použitých bodů na „kvalitu“ pozdější rekonstrukce, bohužel se nám nepodařilo „vyřadit nepovedené“ body, které vnášejí chybu.

Provedeme transformaci souřadnic námi (projektivně) rekonstruované scény na souřadnice v reálné („skutečné“) scéně: X_i=H^-1. m_i.myX_i a zobrazíme ve 3D (v obrázku: oooo).

Analogicky s bodem 4, 5 pomocí nových projekčních matic myP, myP’ provedeme zpětnou projekci „skutečné“ scény do obrazu a zobrazíme (v obrázku: oooo).

 

Naše implementace

1.   Postup našeho výpočtu je uložen v souboru uloha2.m.

Ukázka postupu

Vstupní obrazy

 

 

Vstupní obrazy s korelujícímy body, epipolárami, epipóly a všemi zpětnými projekcemi

 

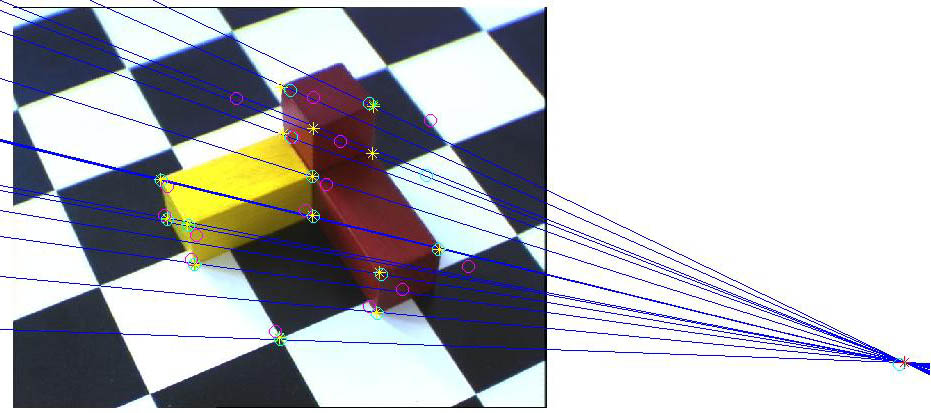
Skutečná a (projektivně) rekonstruovaná scéna

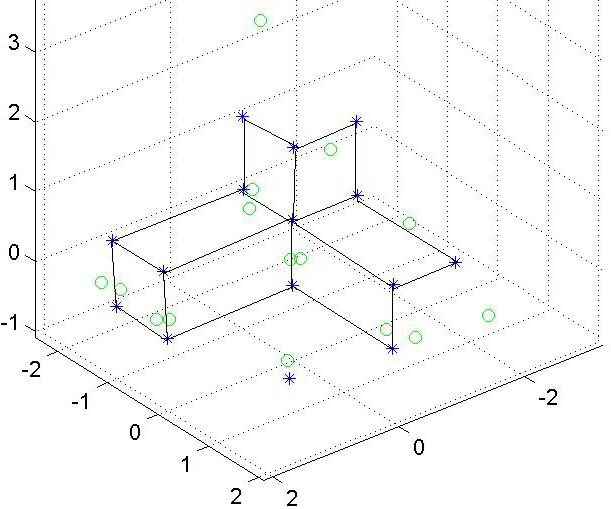
Závěr

Použitím skriptu v souboru uloha2.m lze předvést všechny požadované funkce týkající se rekonstrukce scény.

Kvalita rekonstrukce bohužel není nejlepší, neboť celkový výsledek poškodí několik „špatných“ bodů, které se nám nepodařilo (zcela) odstranit.