![]() ,
,
Vladislav Němec, 433
Zadání
Úkolem této úlohy byla rekonstrukce prostorové scény ze dvou zadaných
obrazů sejmutých kamerou při zadané známé korespondenci mezi body.
1) Výpočet epipolární geometrie
Nejprve je třeba vypočítat fundamentální matici pro zadané pohledy. Pro tuto matici platí
![]() ,
,
kde ![]() je (řádkový) vektor homogenních souřadnic bodu v prvním obraze
je (řádkový) vektor homogenních souřadnic bodu v prvním obraze ![]() ,
,
![]() je (sloupcový) vektor homogenních souřadnic odpovídajícího bodu ve druhém
obraze
je (sloupcový) vektor homogenních souřadnic odpovídajícího bodu ve druhém
obraze 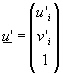 .
.
F je fundamentální matice dvojic obrazů.
Ze vztahu
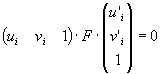
vyjádříme pro každý bod jednu rovnici. Jelikož matice F je typu 3x3 a rovnice je homogenní, je třeba minimálně osmi bodů, abychom obdrželi právě jedno řešení. Při použití více než osmi bodů musíme snížit hodnost sestavené rovnice na 8.
![]()
![]()
![]() reprezentuje přímku (epipoláru) v prvním obraze
reprezentuje přímku (epipoláru) v prvním obraze
![]() reprezentuje přímku (epipoláru) v druhém obraze
reprezentuje přímku (epipoláru) v druhém obraze
Pomocí matice ![]() , můžeme body z prvního obrazu zobrazit na přímku (epipoláru) do obrazu
druhého a naopak. Pro body na spojnici středů kamer nemá přímka reprezentanta
(0, 0, 0). Rovnice epipólů (průsečíky epipolár) tedy získáme z rovnic :
, můžeme body z prvního obrazu zobrazit na přímku (epipoláru) do obrazu
druhého a naopak. Pro body na spojnici středů kamer nemá přímka reprezentanta
(0, 0, 0). Rovnice epipólů (průsečíky epipolár) tedy získáme z rovnic :
![]()
Zde dostáváme další požadavky na matici F- matice F musí být singulární a mít hodnost 2. Protože je ve většině případů zadávání bodů nepřesné, musíme matici F snížit . Pro korespondující body získané pomocí modulu corrgui vypočteme epipoláry a následně epipóly . V našem případě jsme použili 9 a 11 bodů získaných z následujících vstupních obrazů:


Zobrazení epipolár a epipolů pro devět zadaných bodů je na dvou následujících obrázcích:


Na prvním ze zobrazených obrázků je patrné, že se epipoláry protínají
v nekonečnu.
Zobrazení pro jedenáct korespondujících bodů je na následujících obrázcích:
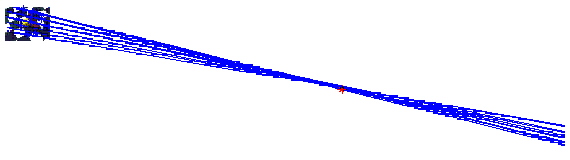

2) Rekonstrukce z kalibrovaných kamer
Výpočet souřadnic bodů skutečné scény provedeme z násleudjících rovnic :
![]() , kde
, kde
![]() jsou konstanty specifické pro každý bod
jsou konstanty specifické pro každý bod
![]() jsou homogenní souřadnice bodů v obrazech
jsou homogenní souřadnice bodů v obrazech
![]() jsou známé (zadané) známé projekční matice
jsou známé (zadané) známé projekční matice ![]()
![]() souřadnice bodů
souřadnice bodů 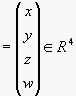 ,
,
je-li ![]() vlastní bod, pak
vlastní bod, pak ![]() a tedy
a tedy
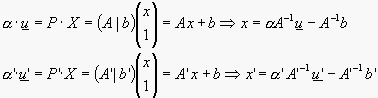
Jelikož je však výpočet numericky nepřesný, chceme minimalizovat příčku mimoběžek
![]()
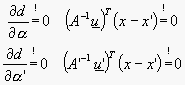
![]()
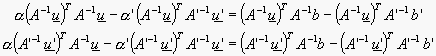
Z těchto rovnic vypočteme ![]() a následným dosazením
a následným dosazením ![]() . Rekonstruovaný bod pak bude ležet ve středu úsečky zadané body
. Rekonstruovaný bod pak bude ležet ve středu úsečky zadané body ![]() a
a ![]() . Grafické znázornění situace je na následujícím obrázku:
. Grafické znázornění situace je na následujícím obrázku:
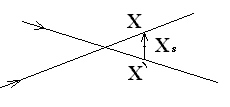
Promítnutí rekonstruovaných hodnot do původního obrazu je na následujícím obrázku - červený bod znázorňuje původní (zadané) hodnoty, tyrkysové kružnice znázorňují námi rekonstruované body. Opět nejdříve pohledy pro devět korespondujících bodů:
Následují obrázky pro 11 korespondujících bodů:
Prostorové znázornění scény je na následujících obrázcích (nejdříve opět obrázek pro 9 korespondujících bodů):
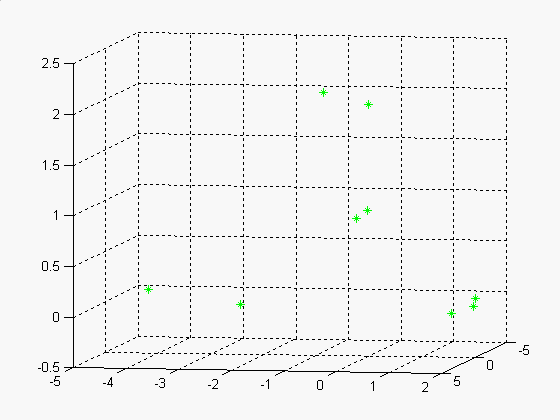
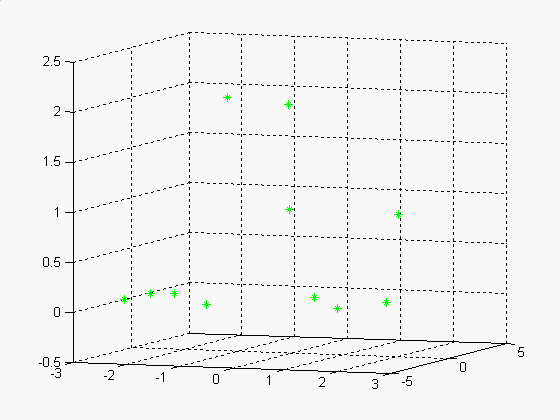
Prostorové znázornění scény je na následujících obrázcích (nejdříve
opět obrázek pro 11 korespondujících bodů):
3) Projektivní rekonstrukce
Při výpočtu opět vycházíme ze známých rovnic, nyní však neznáme projektivní matice P.
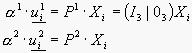
Protože známe vztah mezi projekčními maticemi, můžeme jednu z matic zvolit a sruhou dopočítat .V našem případě jsme zvolili matici jednoduchou (šlo o matici reprezentující identitu - rekonstrukce bude probíhat v souřadné soustavě první kamery). Nyní musíme dopočítat matici druhou.
Matici ![]() lze rozložit na submatici
lze rozložit na submatici ![]() a sloupcový vektor
a sloupcový vektor ![]()
![]() .
.
Jelikož obrazem středu první kamery v druhém obraze je epipól ![]()
![]() a jelikož
a jelikož 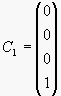 (vzhledem k volbě matice
(vzhledem k volbě matice ![]() ), je sloupcový vektor
), je sloupcový vektor ![]() roven
roven ![]() . Dále lze ukázat, že součin
. Dále lze ukázat, že součin ![]() je antisymetrická matice
je antisymetrická matice
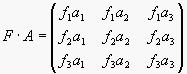 , kde
, kde
![]() je i-tý řádek matice
je i-tý řádek matice ![]()
![]() je i-tý sloupec matice
je i-tý sloupec matice ![]() .
.
Z podmínky antisymetrie předchozí matice dostaneme soustavu rovnic pro výpočet matice A.
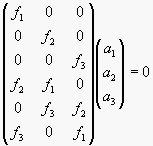
Jelikož hodnost matice předchozí soustavy rovnic je 5, obdržíme čtyřrozměrný systém řešení. Matici A pak dostaneme jako libovolnou lineární kombinaci bázových matic takovou, že hod(A) je 3. Pro lepší numerické výsledky jsem v cyklu vybíral náhodné lineární kombinace a použili jsme kombinaci s největším poměrem prvního a posledního prvku diagonály matice s při svd rozkladu matice A (Singular Value Decomposition). Druhou projekční matici pak složíme z matice A a druhého epipólu
![]()
Z vypočtených projekčních matic můžeme jako v předchozím bodě pomocí
příčky mimoběžek určit rekonstruované body. Přesnost
výpočtu není v tomto případě nijak veliká, pro naše potřeby je ale dostačujácí.
**** toto místo postupu je (jak bude ozřejmeno dále) vhodné označit
Mezi skutečnými a rekonstruovanými body platí, že jsou stejné až na vynásobení maticí 4x4 (stejnou pro všechny body) a kostantou specifickou pro každý bod
![]()
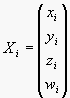
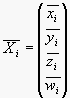
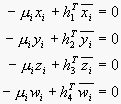

Z tohoto vztahu můžeme vypočítat matici H.
Tuto pasáž (počínaje výše inzerovaným označením ****) jsme bohužel nestihli zrealizovat, takže výsledné zobrazení bodů do prostoru eufemicky řečeno "ne zcela vystihuje situaci". Tato deformace se dotýká pouze prostorového zobrazení, takže zobrazení bodů do plochy původního obrazu odpovídá skutečnosti.
Výsledek je možné posoudit na následujících obrázcích (opět v pořadí
9 a 11 korespondujících bodů):
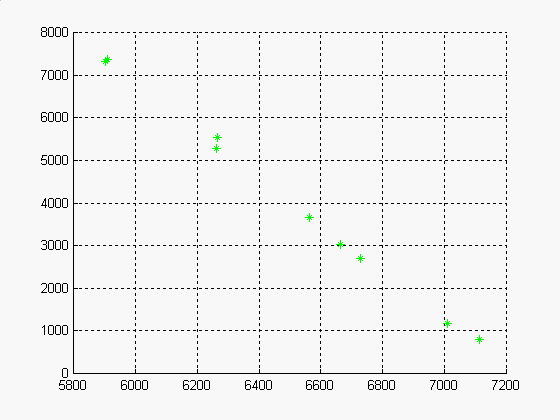
Rekonstruované body v 1. pohledu za pomocí námi vypočtené projektivní
matice pro 9 bodů
Rekonstruované body do v 2. pohledu za pomocí námi vypočtené projektivní matice pro 9 bodů
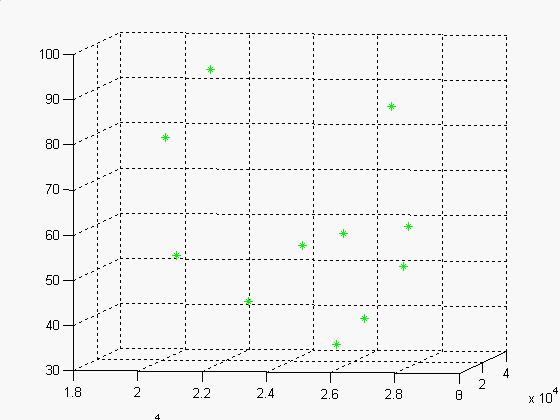
Rekonstruovaná 3D scéna za pomoci námi vypočtených projektivních matic
pro 9 bodů
Rekonstruované body v 1. pohledu za pomocí námi vypočtené projektivní
matice pro 11 bodů
Rekonstruované body do v 2. pohledu za pomocí námi vypočtené projektivní
matice pro 11 bodů
Rekonstruovaná 3D scéna za pomoci námi vypočtených projektivních matic
pro 11 bodů
Závěr
Z vypočítaných hodnot vyplývá, že roustoucí počet korespondujících
bodů způsobuje přesnější výpočet epipólů (protože pro jejich výpočet máme
k dispozici více údajů), při výpočtu epipolár dochází k chybě větší, protože
vycházíme z matice reprezentující všechny body a chyba se tedy "nasčítává".
Ke stejnému jevu dochází i při výpočtu 2D a 3D rekonstrukce. Domníváme
se, že rekonstrukce s pomocí námi určených projekčních matic poskytuje
horší výsledky než rekonstrukce z projekčních matic zadaných, protože náš
postup určuje klíčovou hodnotu v iterovaném cyklu za použití náhodného
vektoru.