Rekonstrukce

Předmět:              Počítačové vidění pro informatiku

Student:                              Michal Stránský, Jan Koutník

Teorie

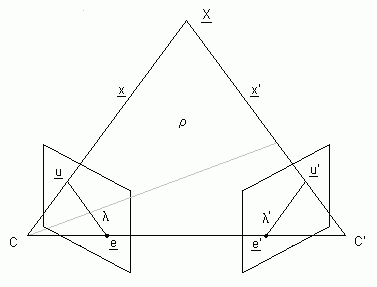
Úkolem rekonstrukce je ze dvou nebo více snímků sestrojit rekonstrukci prostorové scény, tedy získání projekčních matic a souřadnic bodů ve scéně. V této úloze jsou uvažovány pouze dva snímky. Základem pro rekonstrukci je zjištění epipolární geometrie. V podstatě epipolární geometrie popisuje vztahy bodů zobrazených ze scény mezi jednotlivými snímky, a vychází z faktu, že  bod ve scéně, jeho dva obrazy ve dvou snímcích a středy kamer leží všechny v jedné rovině. Pro každý bod ve scéně který neleží na přímce určené středy kamer lze sestrojit přímku v jednom snímku která je obrazem promítacího paprsku tohoto bodu ve druhé kameře, tato přímka se nazývá epipolára, Jelikož všechny tyto promítací paprsky procházejí středem kamery, budou se i jejich obrazy (epipoláry) protínat v jednom bodě—epipólu. Tento epipól obecně nemusí ležet v oblasti snímku, může v některých případech dokonce ležet v nekonečnu.

Epipolární geometrie můžeme matematicky popsat takto: Nechť C a C’ jsou středy první a druhé kamery, x je bod ve scéně (ve světových souřadnicích, nechť je střed první kamery počátek, báze světového souřadného systému je ztotožněna s bází první kamery) T=C‘-C. Obrazy u a u‘ jsou obrazy v kamerách 1 a 2 v homogenních souřadnicích (ò) snímků. Pak:

                  (r1)

(r2)

kde K a K’ jsou kalibrační matice kamer, R je rotační matice z báze první kamery do báze druhé. Jelikož musí středy kamer a bod ve scéně ležet v jedné rovině musí platit totéž pro vektor x (vektor od středu první kamery do bodu scény), vektor x’ (vektor od středu druhé kamery do bodu ve scéně) a vektor T (vektor od středu první kamery do středu druhé). Leží-li tři vektory v E³ v jedné rovině pak smíšený součin je rovný nule, tj. x×(T´x’)=0. Vektory x resp. x’ se dají inverzní transformací vyjádřit z obrazů u a u‘ v homogenních souřadnicích. Vektorový součin T´x’ se dá vyjádřit jako maticový součin S(T)x’ kde S(T) je antisymetrická matice vyjádřená takto:

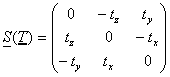
a celá rovnice se dá přepsat na (K^-1u)^T(S(T)R^-1K‘^-1u‘)=0 neboli u^T K^-TS(T)R^-1K‘^-1u‘=0.  Kde výraz
K^-TS(T)R^-1K‘^-1 je matice 3x3 a nazývá se fundamentální matice F, a rovnici pro vztah obrazů bodů pak napíšeme jednoduše:

.    (r3)

Matice F má teoreticky hodnost 2 jelikož matice S(T) má hodnost 2, rotační a kalibrační matice mají  plnou hodnost 3. Jelikož odvození bylo provedeno pro jeden, ale libovolný bod scény (neležící na spojnici středů kamer), bude rovnice platit i pro jiné dvojice korespondujících bodů, proto v rovnici 3 byl souřadnicím v obrazech přiřazen index i. Rovnice 3 se dá rozepsat trochu jinak, pokud dvojice korespondujících bodů v prvním a druhém obraze jsou u_i=(u_i,v_i,1)^T a u_i’= (u_i^’,v_i^‘,1)^T a matice F se rozepíše po členech do sloupcového vektoru:

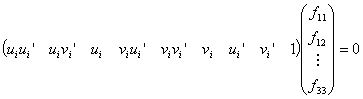.            (r4)

Rovnice 4 má platit pro všechny korespondující body s indexem i současně, tudíž se pro každou korespondující dvojici připíše řádek a rovnice se řeší současně. Vznikne tak soustava A.f^~=0. V rovnici 3 a 4 lze vidět, že se matice F dá určit až na multiplikativní násobek, tudíž řešení soustavy rovnic musí mít dimenzi 1, na to je třeba, aby matice soustavy A měla hodnost 8 jelikož F má 9 prvků. To se ale těžko dá zařídit tak, že se soustava postaví z osmi dvojic korespondujících bodů, což může vézt sice k „numerické“ hodnosti 8 ale „morální“ hodnosti menší, protože body mohou být zvoleny nevhodně (nějak závisle). Proto byla soustava přeurčena a rovnice vyřešena pomocí SVD dekompozice. Metoda SVD která rozloží mxn matici nad reálnými čísly na součin matic UDV^T  kde U je rotační matice mxm, V je rotační matice nxn a D je diagonální matice mxn s prvky na diagonále kladnými nebo nulovými a od levého horního rohu dolů seřazeny sestupně. Pro minimální odlišnost dvou matic se dá použít míra která, dvěma maticím přiřadí číslo, které je součet kvadrátů členů rozdílové matice.  Pro takto navrženou míru se dá ukázat, že minimální odlišnost matice původní od matice s hodností 8, se dá zajistit vynecháním nejmenšího diagonálního členu matice D. Ještě jednodušeji pak vyplyne řešení homogenní soustavy s takto modifikovanou maticí soustavy: báze jednodimenzionálního prostoru řešení je devátý sloupec matice V. Protože by takto navržená matice soustavy obsahovala veliká čísla a členy které mají v ní byt teoreticky nulové by se po aproximaci mohly dramaticky lišit od nuly, je nutné souřadnice ve snímcích normalizovat tak, že střední hodnoty souřadnic zadaných bodů jsou nulové a směrodatná odchylka v jednotlivých směrech je co nejblíže jednotková. Toto se dá u obou snímků zajistit transformací:

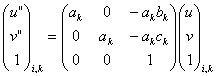                     (r5)

kde:

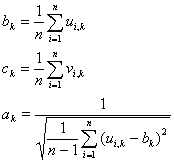
kde n je počet dvojic odpovídajících bodů, dále bylo změněno značení souřadnic v obrazech tak, že souřadnicím z u_i odpovídají souřadnice s k=1 a souřadnicím z u’_i  odpovídají souřadnice s k=2, pak u”_i,k v“_i,k jsou normalizované souřadnice i-té dvojice bodů v k-tém snímku. Označí-li se normalizační matice pro první resp. druhý snímek L₁ resp. L₂ , pak se vypočítá fundamentální matice v normalizovaných souřadnicích F’ výše naznačeným způsobem  podle soustavy sestavené na základě r4 použijí-li se místo původních u a v normalizované u” a v“. Výsledná matice F se spočítá jako:

F=L₁^TF’L₂ .        (r6)

Výše bylo uvedeno že matice F má hodnost 2, ale zde díky nepřesnosti měření nejspíše nalezneme matici s hodností 3, matice F’ se dá podrobit SVD dekompozici a na místo nejmenšího singulárního čísla se dá dát nula, což možná není nejkorektnější ale ono singulární číslo skutečně vycházelo velice blízko k nule.

Souřadnice epipólů ve snímcích se dají vypočítat z fundamentální matice (pokud má hodnost 2) jelikož epipól v jednom obraze nemá odpovídající bod v obraze druhém (střed kamery se nezobrazí tj. P^kC^k=0 )  tj. epipól v prvním obraze odpovídá nulovému prostoru matice F^T epipól v druhém nulovému prostoru matice F. Jelikož se hodnost matice F zaručovala za pomocí SVD, lze epipóly v prvním resp. druhém obraze vybrat z matice U resp. matice V (vždy 3-tí sloupec). Rovnice epipolár se dají také určit z fundamentální matice, protože zobrazený bod leží na epipoláře a relace náležení bodu přímce odpovídá skalárnímu součinu bodu a přímky rovnému nule, což je přesně jeden ze součinů v rovnici r3. Takže koeficienty přímky epipoláry au+bv+c=0 procházející obrazem i-tého bodu v prvém resp. druhém obraze jsou obsaženy ve vektoru F.u_i’ resp. F^T.u_i .

Rekonstrukce z kalibrovaných kamer

Jeli známa fundamentální matice F , souřadnice korespondujících bodů v obrazech, kalibrační matice kamer, a báze ve scéně, lze z těchto údajů vypočítat projektivní matice P a P^‘ a skutečné souřadnice bodů ve scéně které odpovídají obrazu tak, že $ a,a’ ¹0 ÎÂ , XÎÂ⁴ , au=PX, a’u‘=P’X‘  "u, u‘. Získání projekčních matic euklidovské rekonstrukce je nad rámec této práce, proto byly dodány externě. Získání bodů X ve scéně se pak provede triangulací. Víme, že bod ve scéně by měl ležet v průsečíku projekčních přímek, takže pro každou dvojici korespondujících bodů sestrojíme dvě přímky, každá bude procházet středem kamery a obrazem bodu ve snímku, tyto dvě přímky by se měli protnout v bodě scény který je vzor těchto obrazů. Z důvodu šumu a jiných chyb měření, se tyto přímky nejspíš neprotnou, tudíž za odpovídající vzor se vezme střed příčky mezi těmito mimoběžkami. Jsou-li projekční matice (3x4) ve formě P=(A|b) a P’=(A‘|b’) a bod ve scéně popsán vektorem (x,y,z,1)^T , jeho obrazy (u,v,1)^T , (u’,v‘,1)^T pak lze projekční paprsky z první resp. druhé kamery vyjádřit jako: x=aA^-1u-A^-1b resp. x’=a‘A‘^-1u‘-A‘^-1b‘.

Minimalizací lze nalézt dva bodu na těchto paprscích tak, že jejich vzdálenost d=|x-x‘| je minimální, tyto body leží na příčce mimoběžek. Derivace d podle a a a’ se položí rovny nule a se sestaví systém rovnic o neznámých a a a’:

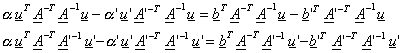   (r7)

Z a,a’ se vypočítají krajní body příčky x a x’ a za rekonstruovaný bod se bere střed (x + x’)/2.

Projektivní rekonstrukce

Jeli známa fundamentální matice F , souřadnice korespondujících bodů v obrazech, lze z těchto údajů vypočítat nějaké projektivní matice P a P^‘ a  body X  které odpovídají obrazu tak, že $ a,a’ ¹0 ÎÂ , XÎÂ⁴ , au=PX, a’u‘=P’X‘  "u, u‘. Tato rekonstrukce není ale euklidovská, ale je to obecná projektivní rekonstrukce. Rekonstrukci lze provézt i když zvolíme P pevné, rovno (E₃|0). Stačí dopočítat P’,a X. Potřebujeme aby (P.X_i)^TF(P’.X_i)=0  tj.  X_i^TP^T.F.P’.X_i=0. Jelikož P víme a P’ se dá napsat jako (A|b), X_i jako (x_i,x)^T , xÎÂ rovnice se dá přepsat na x_i^TF.Ax_i + x_i^TFbx=0. Pro zvolené P se dá ukázat , že b v P’ je epipól v druhém snímku a F.b=0 tj. x_i^TF.Ax_i=0. Poslední rovnice formou připomíná maticový zápis smíšeného součinu x_i×(c´x_i)=0, neboli aby rovnice platila, musí F.A být antisymetrická matice.

F známe, F má hodnost 2, neznáme A , pro projektivní rekonstrukci musí mít hodnost 3. Zapíši-li A=(a₁,a₂,a₃), 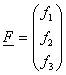, pak z požadavků antisymetričnosti vyplývají požadavky na A ve formě soustavy 6 rovnic o devíti neznámých takto:

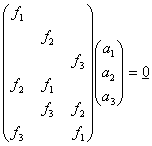,      (r7)

což se dá přeznačit jako W.a=0. Jelikož je hodnost F rovna 2 tak lze ukázat, že matice soustavy v rovnicích r7 má hodnost 5 tudíž řešení soustavy má dimenzi rovnou 4. Bázi řešení lze získat SVD dekompozicí matice W=U.D.V^T, pak čtyři nezávislé vektory řešení a jsou v posledních čtyřech sloupcích matice V, tato řešení se dají přerovnat zpět do tvaru čtvercových matic. Jelikož, o matici A toho moc nevíme, ale chceme aby její hodnost byla 3, musíme najít lineární kombinaci těchto čtyřech řešení takovou aby poměr jejího nejmenšího singulárního čísla ku největšímu byl co největší (tj. aby matice byla co nejdále od singulárnosti). Tohoto bylo ve vypracování této úlohy dosaženo tak, že bylo generováno více náhodných lineárních kombinací, a kombinace s největším poměrem byla uchována.

Rekonstrukce bodů pak byla provedena jako u euklidovské , tj. mezi promítacími paprsky korespondujících bodů byla nalezena příčka, a její střed byl vybrán jako rekonstrukce bodu, je nutné podotknout, že toto není korektní, neb projektivní rekonstrukce nezachovává obecně dělící poměr délek na úsečce.

Nalezení transformace mezi projektivní a skutečnou rekonstrukcí

Mezi skutečnou rekonstrukcí a libovolnou projektivní existuje projektivní transformace H, tak, že $m_i , m_iX_i=HX^s_i  "i, kde X_i jsou souřadnice i-tého bodu v projektivní rekonstrukci scény, X^s_i jsou souřadnice i-tého bodu ve skutečné scéně,  H je matice transfomace (4x4). Je-li P^k projekční matice k-tého zobrazení této projektivní transformace, P_s^k je projekční matice k-té kamery uvedené skutečné rekonstrukce, pak se jednoduše dá ukázat, že platí:g^kP^k  = P_s^k H^-1. Pro výpočet matice H se dá za pomocí výše uvedeného sestavit soustava rovnic, která je  sestavena z odpovídajících bodů rekonstrukcí. Neznámá matice  H reprezentuje základních 16 neznámých,  každým bodem se přidají čtyři rovnice a navíc se přidá jedna další neznámá m_i . Jeli X_i=(x_i,y_i,z_i,w_i)^T a X^s_i =(x^s_i,y^s_i,z^s_i,w^s_i)^T , matice 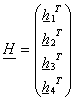 pak jeden bod přidává
rovnice:

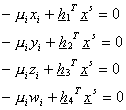       (r8)

Matice H je určena až na multiplikativní násobek tj. hledáme řešení dimenze 1. Pro 5 bodů máme 20 rovnic a 21 neznámých, takže pokud by všechny rovnice byly nezávislé, pak by řešení mělo požadovanou dimenzi, ale opět bylo vybráno více bodů a řešení H bylo určeno SVD dekompozicí.

Příklad aplikace

Pro ilustraci byla v úloze zpracována rekonstrukce ze dvou obrázků kostiček.

1.Výpočet epipolární geometrie

V zadaných obrázcích byla vybrána sada korespondujících bodů, z jejich souřadnic byla s použitím normalizace vypočtena fundamentální matice vypočteny rovnice epipolár příslušných bodů, které byly v obou snímcích zobrazeny jako modré přímky, dále byl  vypočítány a nakresleny pozice epipólů, bohužel jejich pozice v obou snímcích je příliš daleko od okrajů. Navíc je  ve vypočtené fundamentální matici  druhé singulární číslo velice rovno blízce rovno nule . Původní korespondující body byly zvoleny v prostředí „corrgui“ a ve snímcích jsou vykresleny jako modré hvězdičky.

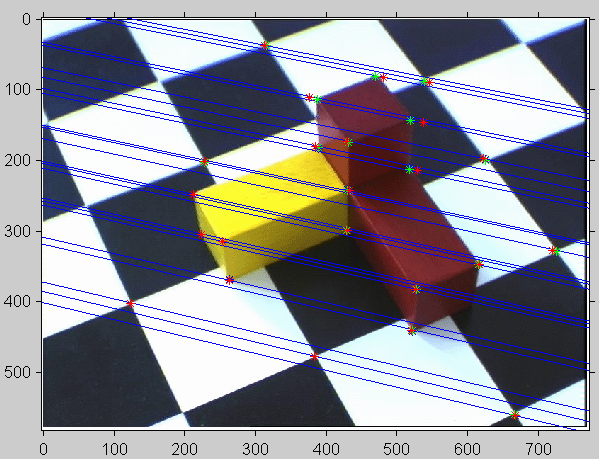
Obr. 1: První snímek

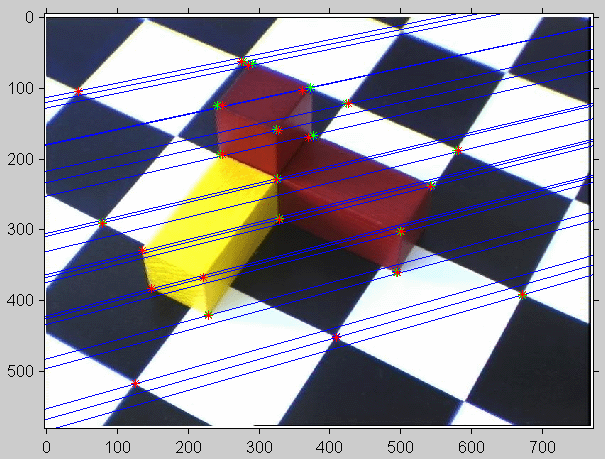
Obr. 2: Druhý snímek

2. Rekonstrukce z kalibrovaných kamer

Protože výpočet projekčních matic euklidovské rekonstrukce je nad rámec úlohy, byly tyto projekční matice zadány, a z nich byly vypočteny souřadnice bodů skutečné scény, ty byly reprojektovány do původních snímků (obr 1 a 2, zelené hvězdičky), a dále byly body zobrazeny v 3D pohledu z částí jako drátěný model (obr 3, modrá barva).

4. Projektivní rekonstrukce

Podle teorie výše byla vypočítána projektivní rekonstrukce, tj. projekční matice a souřadnice bodů, ty byly reprojektovány zpět do původních snímků (obr 1 a 2, červené hvězdičky). Jelikož v předchozím bodě byly vypočítány souřadnice skutečné scény, bylo možno vypočítat matici H transformující mezi skutečnými a souřadnicemi a souřadnicemi z projektivní rekonstrukce. Touto transformací byly zobrazeny body z projektivní rekonstrukce do 3D pohledu v obrázku 3 (zelená barva).

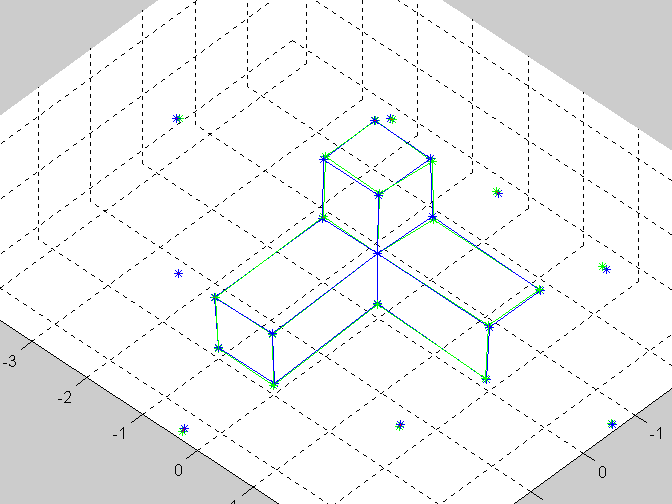
Obr. 3: 3D pohled rekonstrukce scény

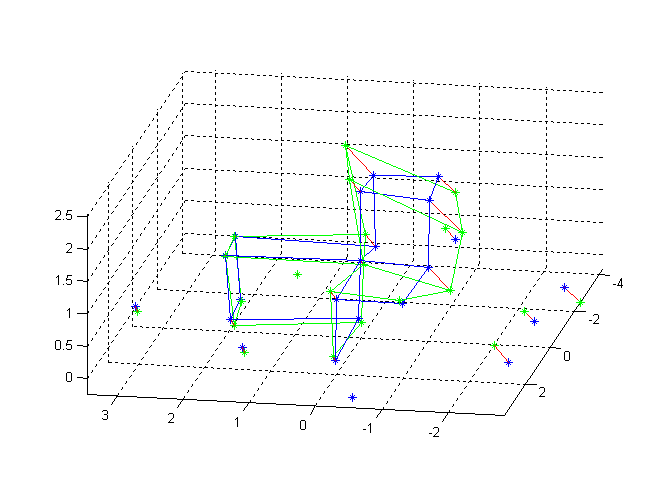
Obr. 4: Jiný pohled do scény

Pro aplikaci metod v této práci byl použit systém Matlab 5.3, hlavní skript lze nalézt v souboru rekonstr.m, který je vám s tímto dokumentem k dispozici. Skript dále používá soubory qmat.m který sestavuje fundamentální matici soustavy, proj.m který trianguluje body ve scéně, projrek.m který spočítá transformační matice projektivní rekonstrukce, hmat.m který zjišťuje transformační matici mezi souřadnicemi skutečné a projektivní rekonstrukce, drawLin.m který vykresluje přímky z rovnic, tyto skripty jsou rovněž k dispozici.

Poznatky a závěr

Numerické chyby při výpočtu fundamentální matice byly částečně eliminovány při použití normalizace. V obou snímcích se polohy epipólů vzdálily od středů snímků. Body zobrazené zpět do původních snímků z projektivní rekonstrukce se přiblížily k původním bodům. Rekonstrukce do 3D pohledu vypadá nejlépe z pohledu uprostřed mezi kamerami (obr. 3 - chyby jsou orientovány ve směru pohledu).

Použité zdroje:

Přednášky předmětu Počítačové vidění pro informatiku, přednášející: Tomáš Pajdla, ČVUT FEL, 1999-2000.