POČÍTAČOVÉ VIDĚNÍ

POČÍTAČOVÉ VIDĚNÍ - PVI

Mozaika z obrazů

Jiří Liška 5/25

Jak spočítám homografii (matici homografie - H)?

Abychom mohli spočítat matici homografie H, musíme znát minimálně 4 různé korespondující body.

pro 4 body plati:

1) ai*ui = H*xi

2) A*h = 0

A je prvkem R(8x9) pro 4 body

hod(A) = 8

pokud máme více bodů:

1) i = 1, ... ,n; n > 4

ui, xi naměříme,

ai(ui + ei) = H*xi; ei ... sum

2) A je prvkem R(2n x 9)

( u1 v1 1 0 0 0 -u1x -v1x -u1 )

A = ( 0 0 0 u1 v1 1 -u1y -v1y -v1 )

( .... )

A nemusi mít hodnost 8, pak existuje řešení h = 0

hledáme přibližné řešení:

A_*h = 0, hod A_ = 8,

A_ blízko A

E = || A_ - A || -> ||E||

řešíme např. pomocí SVD (singular value decomposition):

Nechť A je reálná m x n matice. Pak existují ortonormální matice U = (u1, ... um) je prvkem R(mxn) a V(v1, ... ,vn) je prvkem R(nxn) tak, že U'AV = D; D je diagonálni matice.

A = UDV', kde D = (d1...d9) diagonálni

A_ = UD_V', kde D_ = (d1...d8.0)

v8' = V(:,9)

U(d1...d7.0)(v1';v2';;v8')*h = 0

U(d1...d7.0)(v1';v2';;v8')*v9 = (0;0;;1)

h_=v9 ... vektor

H .. matice (3x3)

H = reshape(h_,3,3)

Výpis skriptu v Matlabu:

I1 = [11.1736 182.2831;

96.2132 271.6142;

156.0559 339.3033;

13.8733 192.4134;

108.8117 293.2563;

129.5091 318.5822;

271.6142];

x-ové souřadnice korespondujících bodů v 1.obrázku a ve 2.obrázku.

I2 = [108.0710 99.3215;

107.6213 86.4352;

97.7278 63.4241;

168.3314 162.3721;

167.4320 151.7870;

181.3728 165.5937;

207.4740];

y-ové souřadnice korespondujících bodů v 1.obrázku a ve 2.obrázku.

im1 = double(rgb2gray(imread('my1.jpg')));

im2 = double(rgb2gray(imread('my2.jpg')));

načítám obrázky

im1 = im1/max(im1(:));

im2 = im2/max(im2(:));

nastavím na hodnoty [0..1]

u1 = [I2(:,1)';I1(:,1)'];

u2 = [I2(:,2)';I1(:,2)'];

u1 = x-ové a y-ové souřadnice bodů korespondence v 1.obrázku

u2 = x-ové a y-ové souřadnice bodů korespondence ve 2.obrázku

figure

nové okno

imshow(im1)

ukaž 1.obrázek

hold

plot(u1(2,:),u1(1,:),'*g')

nakresli body korespondence v prvním obrázku

figure

imshow(im2)

hold

plot(u2(2,:),u2(1,:),'*g')

- nakresli body korespondence ve druhém obrázku

im = zeros(2*size(im1));

vytvoř matici (reprezentující výsledný obrázek) o dvojnásobné velikosti proti původnímu (prvnímu) obrázku

im([1:size(im1,1)]+size(im1,1)/2,[1:size(im1,2)]+size(im1,2))=im1;

nakresli první obrázek do výsledného obrázku na pozice [maxX, maxY/2]

u = u1 + [size(im1,1)/2;size(im1,2)]*ones(1,size(u1,2));

transformace korespondujících bodů v prvním obrázku do výsledného obrázku

figure

imshow(im)

hold

plot(u(2,:),u(1,:),'*g')

kresli body korespondence ve výsledném obrázku pro první obrázek

H = uu2homog(u2,u);

spočítám homografii mezi 2 množinama 2D planárních bodů

v2 = [1 1 ; size(im2,1) 1 ;1 size(im2,2); size(im2)]';

v = p2e(H * e2p(v2));

převod projektivních souřadnic na Euklidovské pomocí matice homografie

plot(v(2,:),v(1,:),'*r')

nakresli jak se promítnou body ve druhém obrázku do výsledného obrázku

b = [floor(min(v')) ceil(max(v'))];

zjisti minimální a maximální bod a zaokrouhli dolů (nahoru)

b = b([1 3 2 4]);

bp = [b([1 3])' b([1 4])' b([2 4])' b([2 3])'];

plot(bp(2,[1:4 1]),bp(1,[1:4 1]),'m')

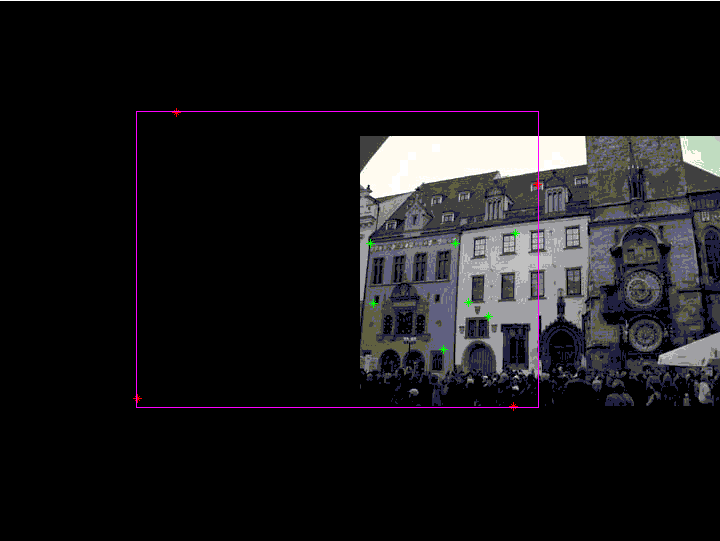
kresli obdélník, který značí, kam se ve výsledném obrázku namapuje druhý obrázek

[y,x] = meshgrid(b(3):b(4),b(1):b(2));

uv = [x(:)';y(:)'];

idx = round(uv(1,:))+round((uv(2,:)-1))*size(im,1);

index ve výsledném obrázku

uv2 = p2e(inv(H) * e2p(uv));

projekční souřadnice výsledného obrázku převede na Euklidovské souřadnice ve 2. obrázku

idx2 = round(uv2(1,:))+round((uv2(2,:)-1))*size(im2,1);

index ve 2.obrázku

ix2 = (uv2(1,:)>=1) & (uv2(1,:)<=size(im2,1)) & (uv2(2,:)>=1) & (uv2(2,:)<=size(im2,2)-20);

nastavi 0 nebo 1 podle toho, zda se může přistupovat indexem do obrázku

im(idx(ix2)) = im(idx(ix2))-im2(idx2(ix2));

rozdílova jasová funkce; jak se liší jas prvního obrázku proti druhému

rozdil = im(305:320,490:505);

našel jsem obdelníkovou oblast, kde se rozdílove hodnoty příliš nemění

rozdil = sum(sum(rozdil)/(size(rozdil,1)*size(rozdil,2)));

průměrná hodnota jasové funkce

im(idx(ix2)) = im2(idx2(ix2))+rozdil;

zapíšu 2. obrázek do druhého a přičtu intenzitu rozdílu

%im(idx(ix2)) = im2(idx2(ix2));

figure

imshow(im)

return
Řešení transformace obrazu metodou nejbližší soused pomocí cyklů:

xm = size (im2, 1)

ym = size (im2, 2)

for x = b(1) : 1.0 : b(2),

for y = b(3) : 1.0 : b(4),

a = p2e (inv(H) * e2p ([x; y]));

if (a(1) >= 1.0 & a(1) <= ym & a(2) >= 1.0 & a(2) <= xm)

i = round (a(1)) + round (a(2) - 1) * size (im2,1);

ii = x + (y - 1) * size (im,1);

im (x + (y - 1) * size (im,1) ) = im2 (i);

end

imshow(im)

p2e

function x = p2e(x_)

%P2E Projective to euclidean coordinates.

% x = p2e(x_) Computes euclidean coordinates by dividing

% all rows but last by the last row.

% x_ ... Size (dim+1,N) Projective coordinates.

% x ... Size (dim,N). Euclidean coordinates.

% (N can be arbitrary.)

if isempty(x_)

x = [];

return;

end

dim = size(x_,1) - 1;

x = x_(1:dim,:) ./ (ones(dim,1)*x_(dim+1,:));

e2p

function x_ = e2p(x)

%E2P Euclidean to projective coordinates.

% x_ = e2p(x) Adds the last row of ones.

% x ... Size (dim,N). Euclidean coordinates.

% x_ ... Size (dim+1,N) Projective coordinates.

% (N can be arbitrary.)

x_ = [x; ones(1,size(x,2))];

uu2homog

function H = uu2homog(u1,u2,s)

%UU2HOMOG Estimates a homography between two planar 2D point sets.

% H = UU2HOMOG(u1,u2) computes the nearest H in LS sense so that

% u2 = p2e( H * e2p(u1) ), (see P2E, E2P)

% where

% H ... Size (3,3). Homography matrix.

% u1, u2 ... Sizes (2,N). Planar point sets in cartesian coords.

% The values u1, u2 must be near 1 for the LS estimator to work properly.

% H = UU2HOMOG(u1,u2,'norm') performs also the normalizations that ensures it,

% or you can use NORMU outside UU2HOMOG.

% See also NORMU.

if size(u1)~=size(u2), error('Bad sizes of input parameters.'); end

N = size(u2,2);

% Normalize u1, u2 so that they are near 1.

% See NORMU for details.

if nargin<3, s = ''; end

if strcmp(s,'norm')

B1 = normu(u1); u1 = p2e(B1*e2p(u1));

B2 = normu(u2); u2 = p2e(B2*e2p(u2));

else

B1 = eye(3);

B2 = B1;

end

% (In the following Eqns we assume that size(u1)=size(u2)=[2 1].)

% The homographic transform can be written as

% [u2; 1] = a*H*[u1; 1]

% After eliminating the scale factor a it can be rewritten as

% u2(1) = H(1,:)*[u1; 1] / H(3,:)*[u1; 1],

% u2(2) = H(2,:)*[u1; 1] / H(3,:)*[u1; 1],

% it can be further written as

% A*reshape(H',9,1) = 0,

% where

% A = [ u1(1) u1(2) 1 0 0 0 -u2(1)*[u1(1) u1(2) 1]

% 0 0 0 u1(1) u1(2) 1 -u2(2)*[u1(1) u1(2) 1] ]

% This homogeneous system of linear eqns is overdetermined for number of

% point pairs > 4.

% For the least squares to work properly, the coords of u1, u2 must

% be near 1 ===> norming u1, u2 needed.

% form matrix A

U1 = [u1' ones(N,1)];

U0 = zeros(size(U1));

A = [ U1 U0 -U1.*(u2(1,:)'*[1 1 1])

U0 U1 -U1.*(u2(2,:)'*[1 1 1]) ];

% Solving the eqns system by SVD or EIG.

% SVD is more stable but prohibitively slow for large number of points.

if 0

% SVD solution

[u,s,v] = svd(A);

Hn_ = v(:,9);

else

% EIG solution

[v,s] = eig(A'*A);

[void,i] = sort(abs(diag(s)));

Hn_ = v(:,i(1));

end

H = inv(B2) * reshape(Hn_,3,3)' * B1;

return