POČÍTAČOVÉ VIDĚNÍ - PVI

Úloha 2: Rekonstrukce scény ze dvou obrazů

Jiří Liška 5/25

Zadání

Naším úkolem byla rekonstrukce scény ze dvou obrazů ze zadaných bodů v obrazech a zadané korespondenci mezi nimi.

1. Výpočet epipolární geometrie

a) fundamentální matice

Nejprve je třeba vypočítat fundamentální matici F ze dvou pohledů. Tato matice definuje epipolární geometrii.

Platí:

,

kde a jsou hohogenní souřadnice bodů v prvním a druhém obraze (u = [ui, vi, 1]), F je fundamentální matice.

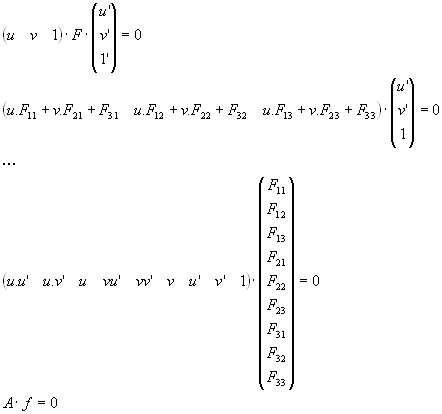
Z tohoto vztahu vyjádříme pro každý bod jednu rovnici. Jelikož matice F je typu 3x3 a rovnice je homogenní, je třeba minimálně osmi bodů, abychom obdrželi právě jedno řešení. Při použití více než osmi bodů musíme snížit hodnost sestavené rovnice na 8. To provedeme pomocí SVD:

[U,S,V] = svd(A);

S(9,9) = 0;

A2 = U*S*V';

f = null(A2);

F = reshape (f, 3, 3)’

, - reprezentuje přímku (epipoláru) v prvním obraze

, - reprezentuje přímku (epipoláru) v prvním obraze

Pomocí matice F můžeme body z prvního obrazu zobrazit na přímku (epipoláru) do obrazu druhého a naopak. Pro body na spojnici středů kamer nemá přímka reprezentanta (0, 0, 0).

Rovnice epipólů (průsečíky epipolár) tedy získáme z rovnic :

b) nakreslené epipoláry a epipóly

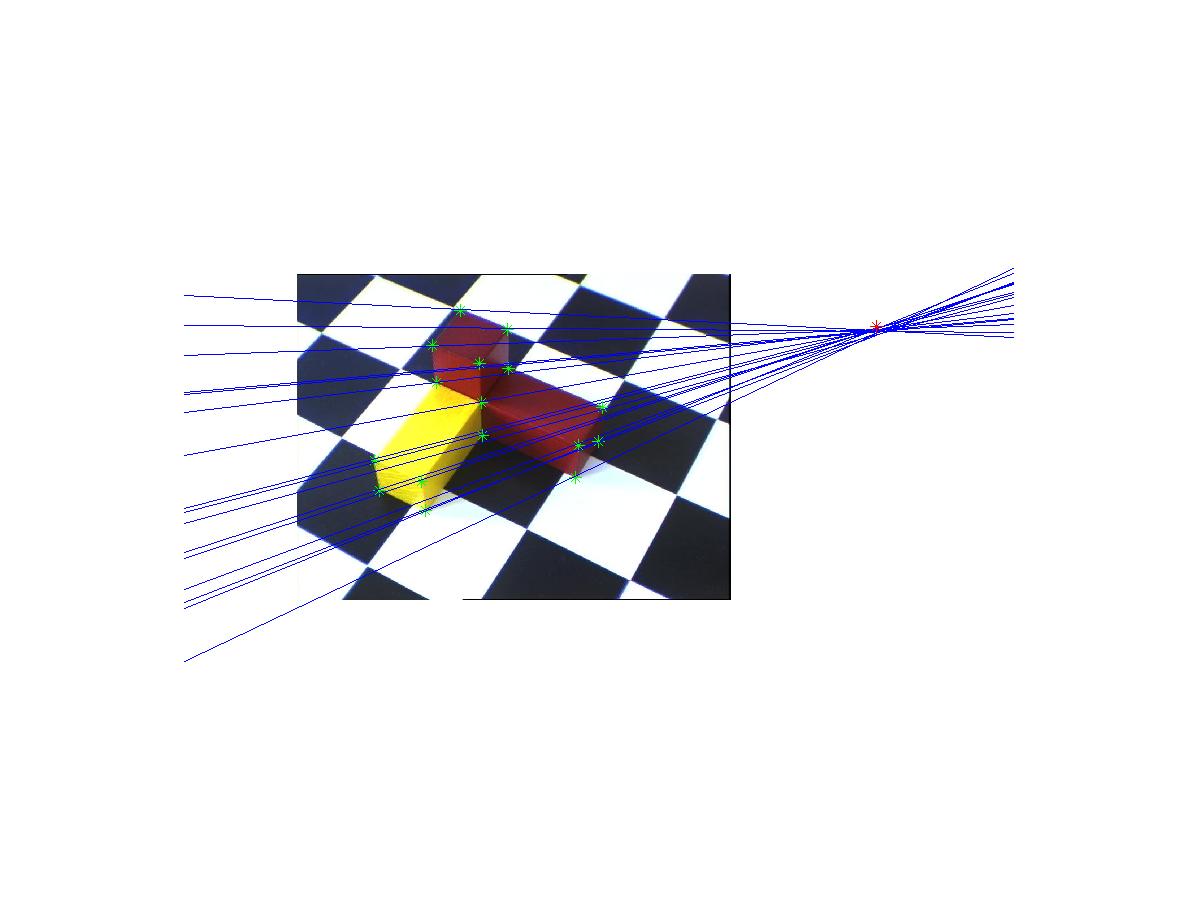
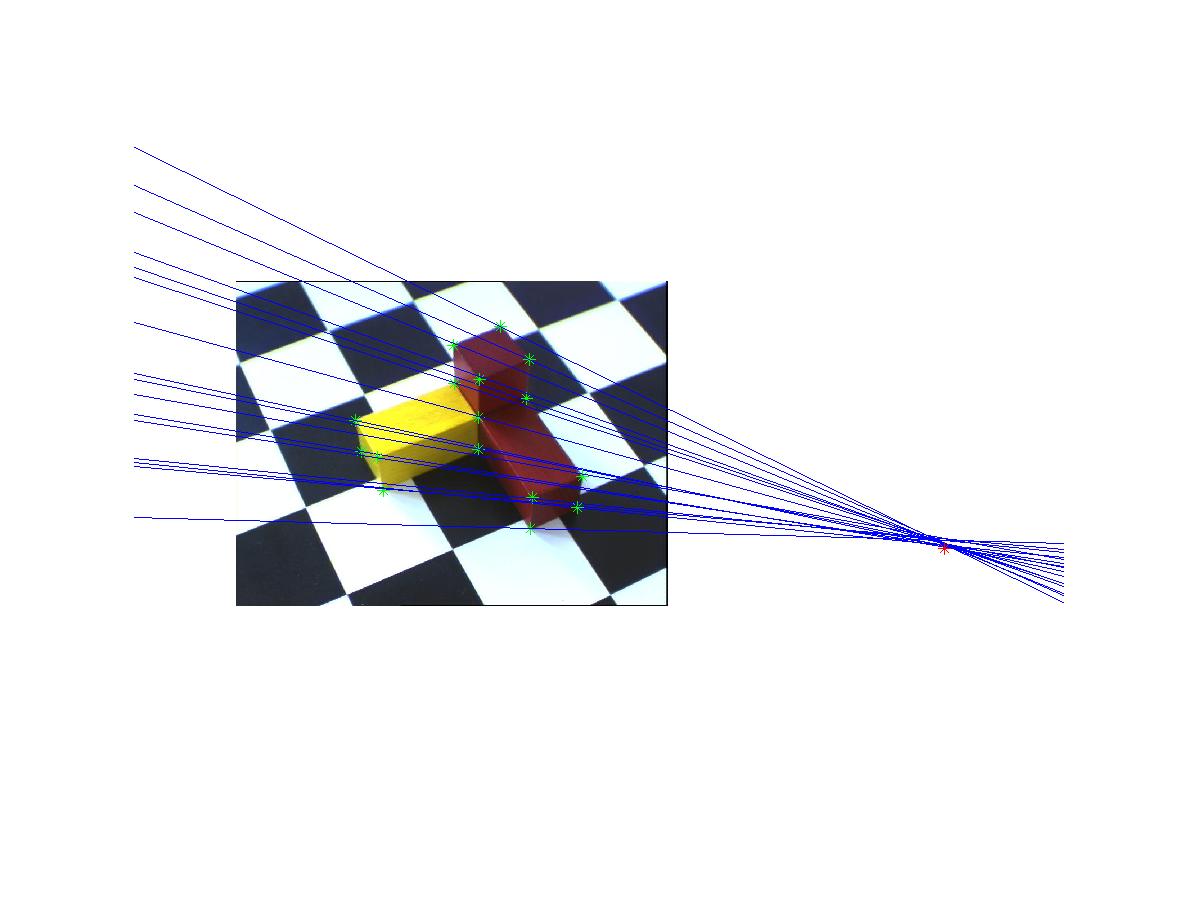
Nalezení epipólů vyšlo trochu nepřesně, což je nejspíš způsobeno tím, že body, které v programu corrgui nalezneme, musíme umístit velmi přesně a protože obrázky nebyly příliš kvalitní a hrany kvádrů byly zaoblené, nepodařilo se mi je umístit přesněji.

2) Rekonstrukce z kalibrovaných kamer

Výpočet souřadnic bodů skutečné scény provedeme z následujících rovnic :

, kde

, jsou konstanty specifické pro každý bod

, jsou homogenní souřadnice bodů v obrazech

, jsou známé projekční matice

, jsou souřadnice bodů

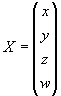
je-li X vlastní bod, pak :

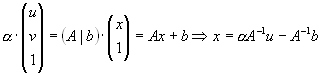
Výpočet je ale numericky nepřesný, protože se přímky nebudou protínat, ale budou mimoběžky, tak chceme nalézt bod, který bude ve středu příčky mimoběžek.

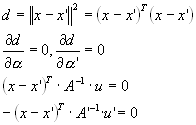
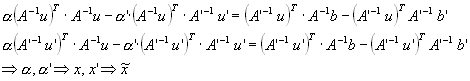
Rekonstruovaný bod bude ležet ve středu příčky zadané body a.

a) reprojekce rekonstruovaných bodů:

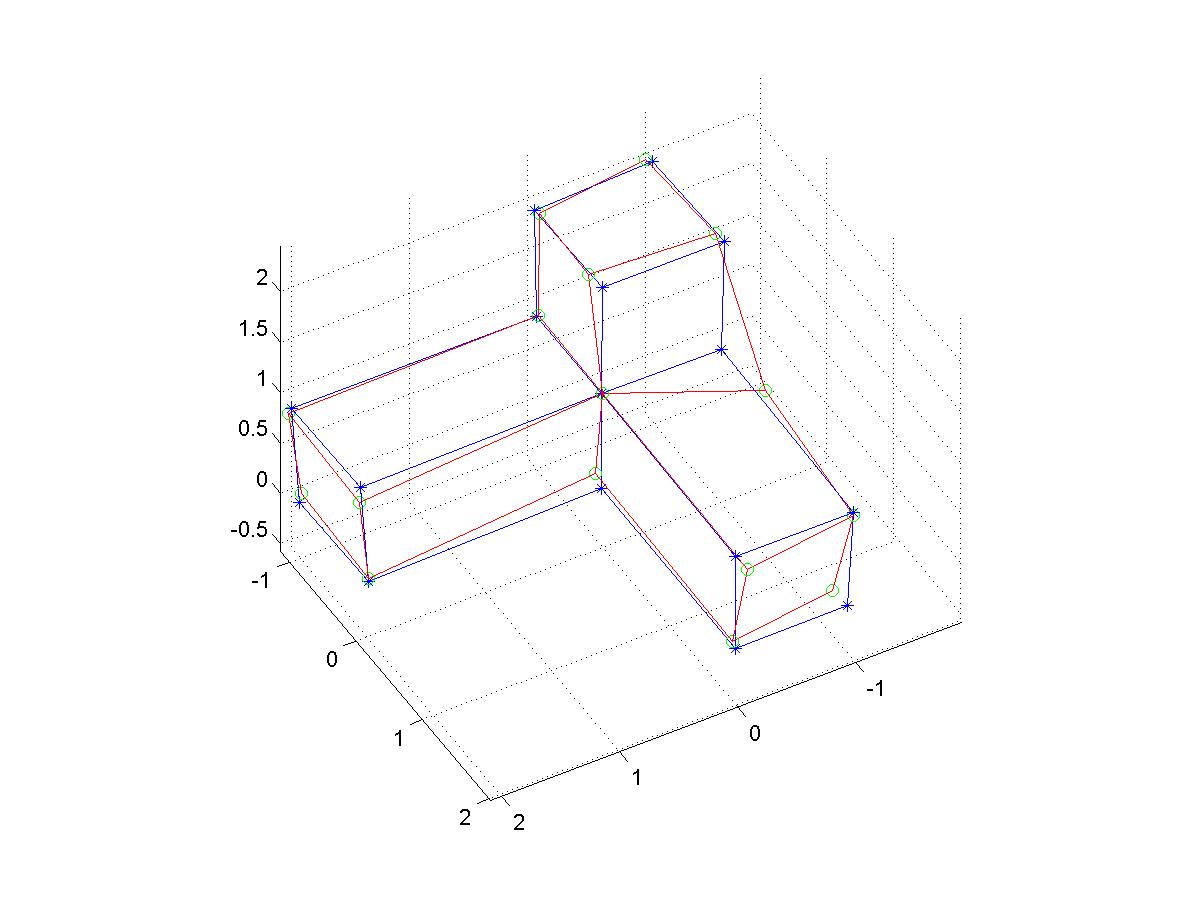
b) pohled na 3D body:

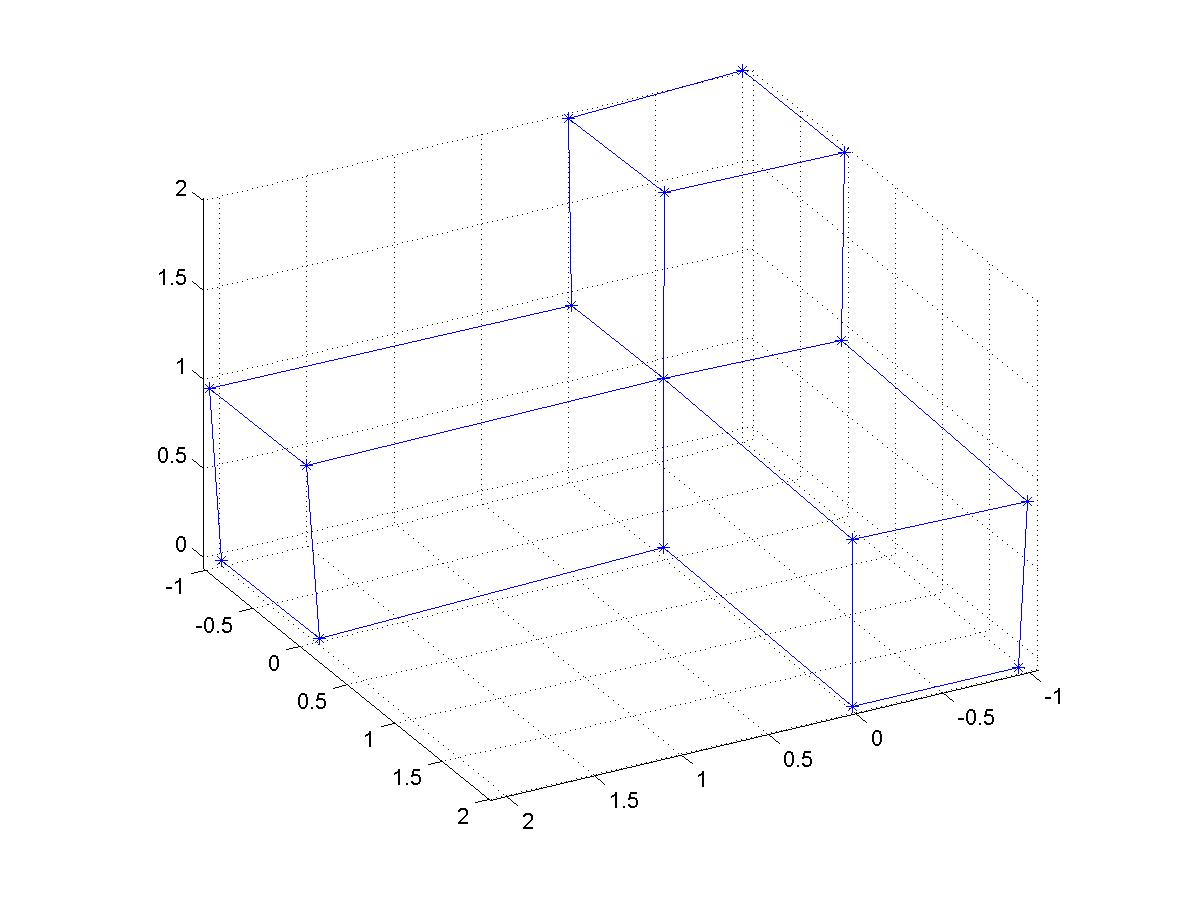
3) Projektivní rekonstrukce

Při výpočtu opět vycházíme ze známých rovnic, nyní však neznáme projektivní matice P.

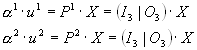
Můžeme jednu matici zvolit a druhou dopočítat, protože známe vztah mezi projekčními maticemi.

Matici P můžeme rozložit na submatici A a sloupcový vektor b

Jelikož obrazem středu první kamery v druhém obraze je epipól e () a , je sloucový vektor b roven . Dále lze ukázat, že součin je antisymetrická matice:

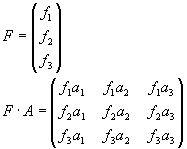
Z podmínky antisymetrie předchozí matice dostaneme soustavu rovnic pro výpočet matice A.

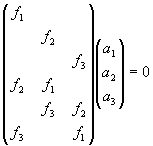
Jelikož hodnost matice předchozí soustavy rovnic je 5, obdržíme čtyřrozměrný systém řešení. Matici A pak dostaneme jako libovolnou lineární kombinaci bázových matic takovou, že hod(A) je 3.

Pro lepší numerické výsledky jsem vybíral z několika náhodných lineárních kombinací a použil jsme kombinaci s největším poměrem prvního a posledního prvku diagonály matice S při svd rozkladu matice A. Druhou projekční matici pak složíme z matice A a druhého epipólu

Z vypočtených projekčních matic můžeme jako v předchozím bodě pomocí příčky mimoběžek určit rekonstruované body.

Mezi skutečnými a rekonstruovanými body platí, že jsou stejné až na vynásobení maticí 4x4 (stejnou pro všechny body) a kostantou specifickou pro každý bod:

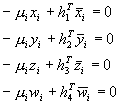
Z tohoto vztahu můžeme vypočítat matici H, potřebujeme ale minimálně 5 bodů.

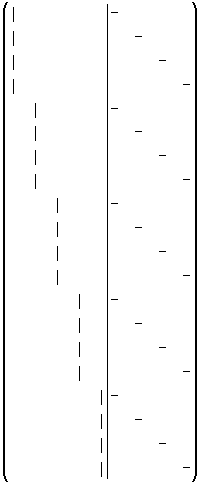
- struktura Z pro 5 bodů

a) reprojekce

b) odhad matice H

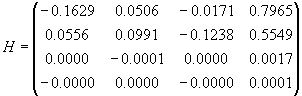
c) 3D pohled na rekonstruované body transformací H