2. Laboratorní práce z PVI – rekonstrukce scény ze dvou obrazů
Vypracoval : Tomáš Polcar 780104/0258
Výpočet epipolární geometrie
Nejprve vypočteme fundamentální matici dvou zadaných pohledů. Pro tuto matici platí :
![]() ,
,
![]() je řádkový vektor souřadnic bodu v prvním obraze
je řádkový vektor souřadnic bodu v prvním obraze ![]()
![]() je sloupcový vektor souřadnic odpovídajícího bodu
v obraze druhém
je sloupcový vektor souřadnic odpovídajícího bodu
v obraze druhém 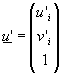
F fundamentální matice dvojice obrazů
Ze vztahu
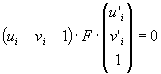
dostaneme pro každý bod jednu rovnici. Jelikož matice
F je typu 3x3 a rovnice je homogenní, potřebujeme minimálně 8 bodů, abychom dostali právě jedno řešení. Použijeme-li více jak 8 bodů, musíme snížit hodnost sestavené rovnice na 8.
![]()
![]()
![]() reprezentant přímky (epipoláry) v druhém obraze
reprezentant přímky (epipoláry) v druhém obraze
![]() reprezentant přímky (epipoláry) v prvním obraze
reprezentant přímky (epipoláry) v prvním obraze
Pomocí matice ![]() , se nám body z prvního obrazu, zobrazí
na přímku (epipoláru) do obrazu druhého a opačně. Pro body na spojnici
, se nám body z prvního obrazu, zobrazí
na přímku (epipoláru) do obrazu druhého a opačně. Pro body na spojnici ![]() (středy kamer), nemá přímka reprezentanta (0, 0, 0). Rovnice epipólů (průsečíky epiporár) tedy
získáme z rovnic :
(středy kamer), nemá přímka reprezentanta (0, 0, 0). Rovnice epipólů (průsečíky epiporár) tedy
získáme z rovnic :
![]()
Z tohoto plyne požadavek, aby matice ![]() byla singulární
s hodností 2. Jelikož, je většinou zadávání bodů nepřesné, musíme
vypočtené matici
byla singulární
s hodností 2. Jelikož, je většinou zadávání bodů nepřesné, musíme
vypočtené matici ![]() , snížit hodnost (např. pomocí svd).
, snížit hodnost (např. pomocí svd).
Pro naklikané body vypočteme reprezentanty přímek a obou epipólů. Výsledné obrázky jsou :
Z obrázků je vidět, že epipól neleží přesně na průsečíku epipolár. Výsledky jsou však velmi přesné. Jestliže bychom chtěli, aby epipoláry procházeli epipólem, museli bychom jejich reprezentanty počítat z upravené matice F s hodností 2.
Rekonstrukce z kalibrovaných kamer
Výpočet souřadnic bodů skutečné scény provedeme z rovnic :
![]()
![]() konstanty specifické pro každý bod
konstanty specifické pro každý bod
![]() souřadnice bodů v obrazech
souřadnice bodů v obrazech
![]() známé projekční matice
známé projekční matice ![]()
![]() souřadnice bodů
souřadnice bodů 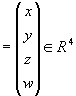
je-li ![]() vlastní bod, pak
vlastní bod, pak ![]() a tedy
a tedy
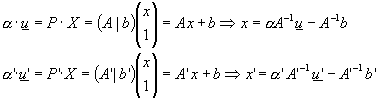
Jelikož je však výpočet numericky nepřesný, chceme minimalizovat příčku mimoběžek
![]()
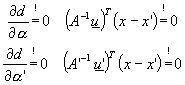
![]()
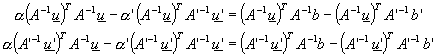
Z těchto rovnic vypočteme
Vypočtený 3D model scény je na tomto obrázku. Zde jsou pak vidět i souřadnice středů kamer (ty získáme
z rovnice ![]() , jelikož víme,
že kamera zobrazuje svůj střed na nulový vektor).
, jelikož víme,
že kamera zobrazuje svůj střed na nulový vektor).
Rekonstruované body promítnuté zpět do obrazu jsou na následujících obrázcích (první, druhý obraz). Je vidět, že červené body (reprojektované) dobře kryjí body zelé (naklikané).
Projektivní rekonstrukce
Výpočet opět zahájíme ze známých rovnic. Nyní však neznáme projektivní matice P.
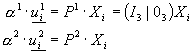
Jelikož je nám jedno, jaké matice
Matici ![]() , lze rozložit na submatici
, lze rozložit na submatici ![]() a sloupcový vektor
a sloupcový vektor ![]()
![]() .
.
Jelikož obrazem středu první kamery v druhém obraze je epipól
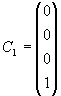 (viz volba matice
(viz volba matice 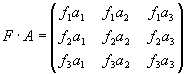
![]() řádek matice
řádek matice ![]()
![]() sloupec matice
sloupec matice ![]() .
.
Z podmínky antisymetrie předchozí matice dostaneme soustavu rovnic pro výpočet matice A.
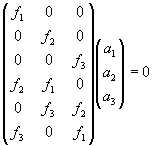
Jelikož hodnost matice předchozí soustavy rovnic je 5, dostaneme 4-dimenzionální systém řešení. Matici A pak dostaneme jako libovolnou lineární kombinaci bázových matic takovou, že hod(A) je 3. Pro lepší numerické výsledky jsem v cyklu vybíral náhodné lineární kombinace (asi 1000 cyklů) a vzal jsem tu, která měla největší poměr posledního a prvního prvku diagonály matice s, při svd rozkladu matice A. Druhou projekční matici pak složíme z matice A a druhého epipólu
![]()
Z vypočtených projekčních matic, můžeme jako v předchozím bodě pomocí příčky mimoběžek, spočítat rekonstruované body. V tomto případě už není tato metoda tak dobrá, ale pro náš přibližný výpočet postačí. Na obrázcích (první, druhý obraz) je vidět větší chyba reprojekce bodů než u kalibrovaných matic (některé modré body vůbec nekryjí zadané body).
Mezi skutečnými a rekonstruovanými body platí, že jsou stejné až na vynásobení maticí 4x4 (stejnou pro všechny body) a kostantou specifickou pro každý bod
![]()
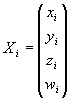
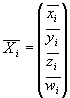
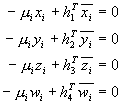

Z tohoto vztahu můžeme vypočítat matici H. Pro jeden bod mám 16+1 neznámých a 4 rovnice. S každým dalším bodem získáme další 4 rovnice a jednu neznámou. Jestliže tedy budeme mít 5 bodů, dostaneme 20 rovnic pro 21 neznámých. Homogení rovnice má tedy jednodimenzionální prostor řešení. Matice soustavy bude mít takovýto tvar. Já jsem pro výpočet použil všechny body (26), které jsem měl k dispozici, takže jsem dostal 104 rovnic pro 42 neznámých. Hodnost matice soustavy jsem snížil pomocí svd na požadovaných 41.
Takto jsme vypočítali matici pro transformaci skutečných bodů do
projektivní rekostrukce. Pro opačnou transformaci předěláme systém rovnic nebo
použijeme ![]() . Rekonstruované
body po transformaci maticí H vypadají ve 3D prostoru takto.
Na tomto obrázku se jeví body jako velmi přesně vypočtené. Je to však pouze volbou
pohledu. Použijeme-li jiný pohled, je vidět, že v zadní
části obrazu je chyba dosti veliká.
. Rekonstruované
body po transformaci maticí H vypadají ve 3D prostoru takto.
Na tomto obrázku se jeví body jako velmi přesně vypočtené. Je to však pouze volbou
pohledu. Použijeme-li jiný pohled, je vidět, že v zadní
části obrazu je chyba dosti veliká.
Výpočet epipolární geometrie a rekostrukce z kalibrovaných kamer se povedl s velmi malou chybou. To přisuzuji velkému počtu (26) poměrně dobře zadaných korespondujících bodů. Větší chyby se začali projevovat u výpočtu obecné rekonstrukce. Velký podíl na chybách připisuji ne zcela oprávněnému použití výpočtu rekonstruovaných bodů pomocí příčky mimoběžek. Dalšího zlepšení bychom patrně dosáhly použitím normalizace a dalších numerických triků (které neznám).