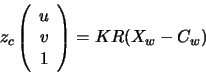 |
(1) |
Josef Šivic
| kde : | |||
| K | je | kalibrační matice kamery | |
| R | je | rotační matice vyjadřující přechod od světových souřadnic | |
| k souřadnicím kamery | |||
| Xw | je | bod vyjádřený ve světových souřadnicích | |
| Cw | je | počátek souřadného systému kamery vyjádřený ve | |
| světových souřadnicích | |||
| (u,v,1)T | je | bod
|
|
Přepíšeme-li bod Xw do homogenních souřadnic, lze pak posunutí mezi počátkem světového systému souřadnic a systému souřadnic kamery vyjádřit pomocí maticového násobení. Rovnici (1) lze pak zapsat jako:
| kde : | ||
|
|
je bod ležící v obrazové rovině, vyjádřený | |
| v homogenních souřadnicích | ||
|
|
je bod světových souřadnic, vyjádřený | |
| v homogenních souřadnicích |
Máme-li tedy dva obrázky scény sejmuté různými kamerami z různých míst a zadáno Nkorespondujících bodů uij ,kde j=1,2,
![]() platí rovnice
platí rovnice
Sejmeme-li podle zadání úlohy obrázky ze stejného místa (ale s možným různým natočením a nakloněním) a ztotožníme-li počátek světového systému souřadnic a systému souřadnic kamery, rovnice
(3) se změní takto
Rovnice (4) lze pak dále upravovat
což lze přepsat jako
Vyjádříme-li z druhé rovnice z (5)
![]() ,
dosadíme
výsledek do první rovnice z (5) dostaneme
,
dosadíme
výsledek do první rovnice z (5) dostaneme
Po zavedení
![]() a
H=K1R1(R2)-1(K2)-1dostaneme hledaný vztah mezi korespondujícími body ve dvou obrazech sejmutých z
jednoho místa
a
H=K1R1(R2)-1(K2)-1dostaneme hledaný vztah mezi korespondujícími body ve dvou obrazech sejmutých z
jednoho místa
Úkolem je tedy nalézt zobrazení
![]() .
.
Rovnici (7) lze přepsat jako
Po úpravách rovnice (8 dostaneme pro každý bod
![]() dvojici rovnic
dvojici rovnic
Takovouto soustavu lze převést do maticového tvaru
Aby byla soustava (10) řešitelná, potřebujeme znát alespoň 4 korespondující
body.
Známe-li právě 4 korespondující body, hod A=8 a soustava má právě jedno
netriviální jednodimenzionální řešení
![]() .
.
Máme-li více korespondujících bodů, hod A může být 9 a v takovém případě má soustava (10) pouze triviální řešení. Cílem tedy je vhodným způsobem snížit hod A na 8. Jedna z možností je rozložit A pomocí SVD na A=UDVT. Vynulováním nejmenšího singulárního čísla dostaneme matici
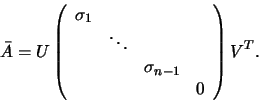
Po dosazení ![]() místo A do (10) dostaneme
místo A do (10) dostaneme
Hledáme tedy takový vektor ![]() ,
který je ortogonální k
,
který je ortogonální k
![]() ,
tj. musí platit
,
tj. musí platit
![]() pro
pro
![]() .
Na ortogonalitě k
.
Na ortogonalitě k ![]() nezáleží, protože tam je nulovost rovnice zajištěna (
nezáleží, protože tam je nulovost rovnice zajištěna (
![]() ). Je vidět, že řešením je
vektor
). Je vidět, že řešením je
vektor ![]() .
.
Transformační matice má tedy tvar
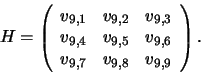
% PVI Uloha 1 - Mozaika
%
% Vstup: 2 obrazky sceny sejmute z jednoho mista: im1, im2
% N korespondujicich bodu: u1 , u2
%
% Vystup: Vysledny obrazek obsahujici slozene obrazky: im
%
% Autor: Josef Sivic
% Datum: 4/4/2000
%nacti obrazky
im1=double(rgb2gray(imread('panorama1.jpg')));
im2=double(rgb2gray(imread('panorama2.jpg')));
im1=im1/max(im1(:));
im2=im2/max(im2(:));
%nacti korespondujici body
load panoramap.mat
%ukaz obrazky a body
imshow(im1)
hold on
plot(I1(:,1),I2(:,1), '*');
figure
imshow(im2)
hold on
plot(I1(:,2),I2(:,2), '*');
%vytvor velky obrazek a uloz do nej prvni obrazek
im=zeros(size(im1)*2);
im( size(im,1)/4+(1:size(im1,1)) ,(size(im,2)-size(im1,2))+1:size(im,2))=im1(:,:);
figure
imshow(im);
%transoformuj souradnice u, do obrazku im
u1=[I2(:,1)' ; I1(:,1)']; %im1
u2=[I2(:,2)' ; I1(:,2)']; %im2
o2=[size(im,1)/4+1,size(im,2)-size(im1,2)+1]; % pocatek im1 v im
u(1,:)=(u1(1,:)+o2(1));
u(2,:)=(u1(2,:)+o2(2));
hold on
plot(u(2,:),u(1,:),'b*')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% matice homografie H: im2 -> im %
% u2 -> u %
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
if 0
%vytvori matici A
N=size(u2,2);
A=zeros(8,2*N);
for i=1:N
A(2*i-1,:) =[u1(1,i) u1(2,i) 1 0 0 0
-u1(1,i)*u2(1,i) -u1(2,i)*u2(1,i) -u2(1,i)];
A(2*i,:)= [0 0 0 u1(1,i) u1(2,i) 1
-u1(1,i)*u2(2,i) -u1(2,i)*u2(2,i) -u2(2,i)];
end;
[V,D]=eig(A'*A);
end
H=uu2homog(u2,u,'norm');
H_=inv(H);
%Transformuj rohy im2 do im v poradi UL, LL, LR, UP
%1.radek radkova souradnic
%2.radek sloupcova souradnice
im2_corn=[1 1; size(im2,1) 1; size(im2,1) size(im2,2); 1 size(im2,2)]';
%transformuj rohy im2 do souradnic im
im2_corn_t=p2e(H * e2p(im2_corn));
plot(im2_corn_t(2,:),im2_corn_t(1,:),'m*');
%opsany obdelnik uvnitr ktereho se pracuje
mir=floor(min(im2_corn_t(1,:)));
mar=ceil(max(im2_corn_t(1,:)));
mic=floor(min(im2_corn_t(2,:)));
mac=ceil(max(im2_corn_t(2,:)));
im2_rect=[mir mic; mar mic; mar mac; mir mac]';
plot(im2_rect(2,[1:4 1]),im2_rect(1,[1:4 1]),':r');
rect=im2_rect;
%%%%%%%%%%%%%%%%%%%%
% Maticovy vypocet %
%%%%%%%%%%%%%%%%%%%%
% vytvor index idx
% pocet sloupcu je stejny jako pocet prvku v opsanem obdelniku
% pocet radku je 2:
% 1. radek je radkovy index prvku opsaneho obdelniku
% 2. radek je sloupcovy index ...
% nezobrazuj posledni sloupce (v obrazku chybi)
mac=mac-10;
% napln pole idx
[rows,cols]=meshgrid(mir:mar, mic:mac);
idx=[rows(:)'; cols(:)'];
% transformace souradnic im do souradnic im2
idx_t=p2e(H_*e2p(idx));
% vybrani jen platnych souradnic, takovych, ktere opravdu lezi v im2
% opsany obdelik pokryva vice
valid=((idx_t(1,:)>=2) & (idx_t(2,:)>=2) &
(idx_t(1,:)<=size(im2,1)) & (idx_t(2,:)<=size(im2,2)));
%%%%%%%%%%%%%%%%%%%%
% prepis im2 do im %
%%%%%%%%%%%%%%%%%%%%
% v idx a idx_t jsou ulozeny souradnice sobe odpovidajicich pixelu v im a im2
% Chceme-li rychle pixely z im2 do im pridat je potreba ze souradnic ve
% forme A(c,r) udelat souradnice a(c*m+r)
% mam-li prvek v matici A na miste A(r,c) (matice ma rozmery (m,n))
% Necht a=A(:), pak A(r,c) je na miste a(c*m + r)
ix=idx(2,:)*size(im,1) + idx(1,:);
ix_t=round(idx_t(2,:)-1)*size(im2,1) + round(idx_t(1,:));
%prepis obrazku
im(ix(valid))=im2(ix_t(valid));
if 0
%vypocet for cyklem
for i=mir:mar %pro vsechny radky z obdelniku v im
for j=mic:mac %pro vsechny sloupce z obdelniku v im
point=p2e(H_*e2p([i j]'));
r=round(point(1));
c=round(point(2));
if (r<=size(im2,1)) & (c<=size(im2,2) & r>=1 & c>=1)
im(i,j)=im2(r,c);
end
end
end
end
% zobraz vysledek
figure
hold on
imshow(im);
axis ij;
![\includegraphics[width=0.8\textwidth]{rec.eps}](img38.gif) |
![\includegraphics[width=0.8\textwidth]{im.eps}](img39.gif) |