Počítačové vidění pro informatiku - Úloha 2
Projektivní rekonstrukce ze dvou pohledů
Josef Šivic
Máte dva obrazy téže prostorové scény sejmuté stejnou kamerou ze dvou různých
míst viz. obr. 1.
- pomocí corrgui zadejte korespondence v obou obrazech
- nalezněte epipolární geometrii
- proveďte rekonstrukci ze zadaných kalibrovaných kamer
- nalezněte projektivní rekonstrukci
- nalezněte transformaci mezi skutečnou scénou (z kalibrovaných kamer) a
nalezenou projektivní rekonstrukcí.
Figure 1:
Vstupní obrázky s vyznačenými 15 korespondencemi
|
Figure 2:
Vstupní obrázky s vyznačenými 25 korespondencemi
|
Mějme dva obrazy téže scény s vyznačenými n korespodujícími body
kde
k=1,2 je počet pohledů(obrazů) a i=1...n je počet bodů.
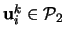 .
Dle [1] str.460-2 lze pro takovouto soustavu bodů odvodit epipolární
geometrii, která je vyjádřena rovnicí
.
Dle [1] str.460-2 lze pro takovouto soustavu bodů odvodit epipolární
geometrii, která je vyjádřena rovnicí
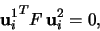 |
(1) |
kde F se nazývá fundamentální matice. Fundamentální matice tedy plně určuje vztah
mezi korespondujícími body ve dvou obrazech. Z rovnice (1) je zřejmé, že 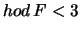 .
[Proč je ale hodnost F právě 2?]
.
[Proč je ale hodnost F právě 2?]
Z rovnice (1) lze také odvodit rovnice epipolárních přímek
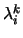 .
.
Vyjdeme z
a
Rovnice epipolár zapíšeme jako
a
Epipóly 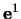 a
a 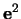 lze spočíst z rovnic
lze spočíst z rovnic
a
Význam epipoláry a epipólu je následující
- Epipolární přímka v prvním obrázku je obrazem spojnice středu druhé
kamery a bodu scény.
- Epipól v prvním obraze je obrazem středu druhé kamery.
Odhad fundamentální matice
Matice F má devět neznámých koeficientů. Napíšeme-li rovnici (1)
pro osum bodů a přepíšeme-li neznámé koeficienty matice F do vektoru
lze pak tuto homogenní soustavu 8 rovnic o 9 neznámých zapsat maticově ve tvaru
Je-li hod A = 8, soustava má jedno netriviální řešení.
V naměřených datech je ale vždy šum, který způsobí, že rovnice (1) neplatí
přesně. Matice 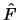 ,
kterou spočteme z osmi naměřených bodů, se od správné
matice F liší. Proto je výhodné matici A sestavit z více než osmi bodů a
hledat řešení této přeurčené soustavy metodou nejmenších čtveců (např. pomocí
SVD, viz.PVI-Úloha č.1). Hodnost spočtené matice
,
kterou spočteme z osmi naměřených bodů, se od správné
matice F liší. Proto je výhodné matici A sestavit z více než osmi bodů a
hledat řešení této přeurčené soustavy metodou nejmenších čtveců (např. pomocí
SVD, viz.PVI-Úloha č.1). Hodnost spočtené matice 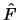 je obecně 3. Aby platila rovnice (1),
je potřeba hodnost
je obecně 3. Aby platila rovnice (1),
je potřeba hodnost 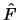 snížit pomocí SVD na 2 (viz.PVI-Úloha č.1). Nesnížíme-li
hodnost
snížit pomocí SVD na 2 (viz.PVI-Úloha č.1). Nesnížíme-li
hodnost 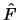 na 2, epipoláry se neprotnou v jednom bodě.
na 2, epipoláry se neprotnou v jednom bodě.
Postup z předchozího odstavce jsme aplikovali na dvě množiny korespondencí. V
prvním přápadě jsme použili 15 bodů (Obr.3) v druhém případě nově
zadaných 25 bodů (Obr.4). Z obrázků je vidět, že v obou případech nám vyšla jiná
epipolární geometrie. Obě řešení mohou být správná. Výpočet epipolární geomterie
ze 7 bodů (nejmenší možný počet bodů) vede totiž na rovnici třetího stupně a ta
může mít až 3 různá řešení.
Figure 3:
Epipolární geometrie získaná z 15 bodů
|
Figure 4:
Epipolární geometrie získaná z 25 bodů
|
Pro bod
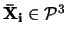 skutečné scény a jeho obraz
skutečné scény a jeho obraz
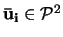 ,
získaný perspektivní kamerou platí zobrazovací
rovnice
,
získaný perspektivní kamerou platí zobrazovací
rovnice
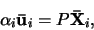 |
(2) |
kde P je
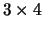 projektivní matice. Odvození viz. [1] str. 449-53.
projektivní matice. Odvození viz. [1] str. 449-53.
Díváme-li se tedy na 3D scénu stejnou kamerou z dvou různých míst, dostaneme pro
každý bod scény, který je vidět oběma kamerami dvě rovnice
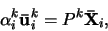 |
(3) |
kde k=1,2.
V našem případě máme změřeny body
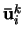 ,
známe projekční matice Pk (z
kalibrace kamer, zadáno) a chceme získat body
,
známe projekční matice Pk (z
kalibrace kamer, zadáno) a chceme získat body
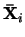 ve scéně a jím
odpovídající koeficienty
ve scéně a jím
odpovídající koeficienty
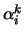 .
Tento problém lze vyřešit
triangulací. Promítneme body
.
Tento problém lze vyřešit
triangulací. Promítneme body
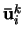 zpětně přes středy příslušných kamer do scény.
Vzniknou tak dvě přímky, které se protnou právě v bodě
zpětně přes středy příslušných kamer do scény.
Vzniknou tak dvě přímky, které se protnou právě v bodě
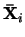 .
V reálném případě jsou naměřené body
.
V reálném případě jsou naměřené body
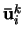 zatíženy šumem a takto
vzniklé přímky se protnout nemusí - mohou být mimoběžné. Bod
zatíženy šumem a takto
vzniklé přímky se protnout nemusí - mohou být mimoběžné. Bod
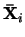 pak získáme jako střed příčky těchto mimoběžek.
pak získáme jako střed příčky těchto mimoběžek.
Viz. sešit.
Triangulací a výpočtem příčky mimoběžek spočítáme rekonstrukci scény z kalibrovaných
kamer (viz obr. 5).
Figure 5:
Čtyři různé pohledy na scénu rekonstruovanou z kalibrovaných kamer
|
Rekonstruované body pro kontrolu promítneme zpět do vstupních obrázků (viz
obr. 6). Zpětně promítnuté body se téměř kryjí s vyznačenými
vstupními body.
Figure 6:
Zpětné projekce scény rekonstruované z kalibrovaných kamer
|
Nemáme-li k dispozici projekční matice kamer ani žádnou apriorní informaci o kamerách
nebo o scéně, můžeme se pokusit spočítat projektivní rekonstrukci. Projektivní
rekonstrukce scény z obrazových bodů
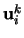 jsou takové dvě množiny
jsou takové dvě množiny
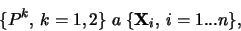 |
(4) |
které splňuje rovnici (3). Lze ukázat, že množiny
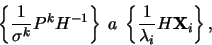 |
(5) |
kde
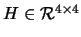 ,
,
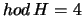 ,
,
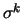 ,
,
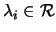 ,
,
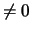 ,
které se liší od (4) o lineární transformaci
H jsou také projektivní rekonstrukcí z bodů
,
které se liší od (4) o lineární transformaci
H jsou také projektivní rekonstrukcí z bodů
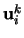 .
.
Dále lze ukázat, že souřadnice 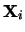 projektivní rekonstrukce se liší od
souřadnic
projektivní rekonstrukce se liší od
souřadnic
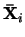 skutečné scény o lineární transformaci
H
skutečné scény o lineární transformaci
H
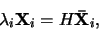 |
(6) |
kde
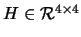 ,
,
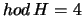 ,
,
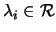 ,
,
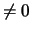 .
.
Dosazením rovnic (3) do (1) dostaneme
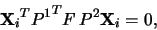 |
(7) |
Naším úkolem je zrekonstruovat matice P1 a P2 tak, aby vyhovovaly rovnicím
(7).
Zvolíme-li P1 ve tvaru
P1=(I|0),
což znamená, že střed první kamery je umístěn v počátku světových souřadnic,
vyjde nám z rovnice (7), že P2 je ve tvaru
P2=(A|e2),
kde
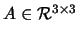 ,
,
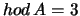 a e2 je epipól v druhém
obraze. Z rovnice (7) dále vyplyne, že platí
a e2 je epipól v druhém
obraze. Z rovnice (7) dále vyplyne, že platí
neboli můžeme říci, že matice FA je antisymetrická.
Rozepíšeme-li podmínku (8) a přepíšeme-li prvky A po sloupcích do sloupcového
vektoru
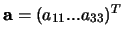 ,
dostaneme lineární soustavu rovnic ve
tvaru
,
dostaneme lineární soustavu rovnic ve
tvaru
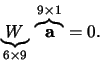 |
(9) |
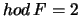 tedy
tedy
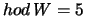 [Proč?] a prostor řešení soustavy (9) má
dimenzi 4. Z prostoru řešení soustavy (9) zvolíme jedno řešení, které
po přeuspořádání do matice A splňuje podmínku
[Proč?] a prostor řešení soustavy (9) má
dimenzi 4. Z prostoru řešení soustavy (9) zvolíme jedno řešení, které
po přeuspořádání do matice A splňuje podmínku
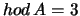 (
(
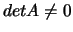 ).
).
Do výpočtu matice A lze závést i podmínku dobré podmíněnosti matice A.
Z prostoru řešení (9) vybereme náhodně mnoho řešení a vybereme
to, pro které je matice A nejépe podmíněná.
[Proč
je dobré, aby byla matice A dobře podmíněná? (špatná podmíněnost =
skoro singularita)]
Znám-li matice P1 a P2, vypočtu z rovnic (3) metodou triangulace a příčky mimoběžek body
projektivní rekonstrukce  .
Výsledky zpětné projekce projektivní
rekonstrukce pomocí spočtených matic P1 a P2 jsou na obrázku 7.
.
Výsledky zpětné projekce projektivní
rekonstrukce pomocí spočtených matic P1 a P2 jsou na obrázku 7.
Figure 7:
Zpětné projekce projektivní rekonstrukce. Body získané zpětnou
projekcí projektivní rekonstrukce jsou označeny křížkem +.
|
Rovnici (6), která určuje vztah mezi skutečnou scénou a její
projektivní rekonstrukcí, přepíšeme do tvaru
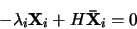 |
(10) |
Soustavu (10) lze dále přepsat jako
Hledáme 16 koeficientů
h11...h44 matice H a koeficient 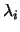 .
Je vidět, že aby existovalo jednodimenziální řešení soustavy (11), potřebujeme alespoň 5
korespondujících dvojic bodů
.
Je vidět, že aby existovalo jednodimenziální řešení soustavy (11), potřebujeme alespoň 5
korespondujících dvojic bodů 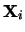 a
a
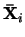 ,
z nichž (myšleno z
každé pětice) jsou každé 4 nekoplanární tzn. neleží v jedné rovině.
Máme tedy soustavu 20 rovnic pro 21 neznámých (16 parametrů hkl a 5 parametrů
,
z nichž (myšleno z
každé pětice) jsou každé 4 nekoplanární tzn. neleží v jedné rovině.
Máme tedy soustavu 20 rovnic pro 21 neznámých (16 parametrů hkl a 5 parametrů
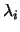 ). Kterou lze přepsat do maticového tvaru
). Kterou lze přepsat do maticového tvaru
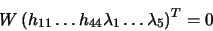 |
(12) |
[Proč nesmí být body koplanární? Vyplývá to z důkazu věty o kolineaci v
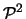 . Geom. smysl?]
. Geom. smysl?]
[Jsou-li čtyři body koplanární (lze říci lineárně závislé tzn. každý lze
vyjádřit jako LK ostních třech ), měla by se nějakým způsobem zredukovat
hodnost W v soustavě (12), JAK ??]
Mám-li k dispozici více než pět bodů nabízí se možnost sestavit přeurčenou
soustavu rovnic (12) a tu pak vyřešit pomocí SVD. Matice W je ale
řídká a proto metoda SVD není vhodná. [Experiment to potvrzuje,
ale proč SVD špatně pracuje s řídkými maticemi?]
Pro výpočet matice H lze použít ještě další metodu.
Aby byla matice H dobře určena, [tzn. popisovala vztah mezi skutečnou
scénou a rekonstrukcí v celém prostoru a ne jen v okolí pěti bodů z kterých
byla spočtena] je potřeba, aby pětice bodů použitých pro výpočet H, byla po
čtveřicích 'co nejméně' koplanární.
Jsou-li 4 body
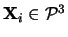 ,
i=1...4 koplanární, pak existuje
rovina
,
i=1...4 koplanární, pak existuje
rovina
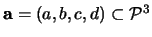 ,
,
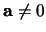 ,
taková že
,
taková že
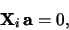 |
(13) |
kde i=1...4.
Soustavu (13) lze přepsat maticově do tvaru
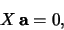 |
(14) |
Míru koplanarity m zvolíme jako číslo podmíněnosti matice X,
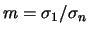 ,
kde
,
kde 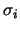 jsou singulární čísla matice X.
Je-li číslo podmíněnosti velké, matice je blízko singularitě a body
jsou singulární čísla matice X.
Je-li číslo podmíněnosti velké, matice je blízko singularitě a body 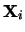 jsou
téměř koplanární. [Dalo by se očekávat, že H nebude dobře zobrazovat
právě ve směru kolmém k takovéto rovině].
Výběr pětice bodů pro výpočet matice H probíhá podle následujícího postupu
jsou
téměř koplanární. [Dalo by se očekávat, že H nebude dobře zobrazovat
právě ve směru kolmém k takovéto rovině].
Výběr pětice bodů pro výpočet matice H probíhá podle následujícího postupu
- Z množiny všech dostupných bodů náhodně vybereme pětici bodů Xi,
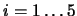
- Spočítáme míru koplanarity mk,
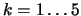 pro všech 5 možných
čtveřic bodů, které lze sestavit z vybrané pětice.
pro všech 5 možných
čtveřic bodů, které lze sestavit z vybrané pětice.
- Jako míru koplanarity m celé pětice bodů vybereme nejhorší kombinaci, tedy
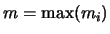 ,
,
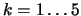 .
.
- Postup opakujeme pro velké množství náhodně vybraných pětic a matici H spočteme z pětice, která má nejmenší m.
Jedná se tedy o minimalizaci nejhorší možné chyby.
Použijeme-li pro odhad matice H z rovnice (12) více bodů a SVD,
výsledky transformace jsou špatné viz obr. (8).
Spočteme-li matici H pomocí rovnice (12) jen z pěti dobře vybraných ('málo koplanárních')
bodů. Výsledky trnasformace jsou podstatně lepší viz obr. (9).
Figure 8:
Pohled na scénu transformovanou maticí H z projektivní
rekonstrukce. Matice H byla spočtena ze všech dostupných bodů metodou SVD.
|
Figure 9:
Čtyři různé pohledy na scénu transformovanou maticí H z
projektivní rekonstrukce. Matice H byla spočtena z pěti bodů s
malou mírou koplanarity.
|
Pro dva zadané obrazy jsme nalezli dvě různé epipolární geometrie, které vznikly
z různého počtu nezávisle zadaných bodů. I když z druhé množiny obsahující 25 bodů
použijeme jen 15 bodů zadaných přibližně na stejných místech jako body první
množiny, epipolární geometrie vyjde stále stejná. Z toho je patrná značná
závislost výpočtu epipolární geometrie na přesnosti zadaných bodů.
Z naměřených dat jsme provedli pomocí triangulace a příčky mimoběžek
rekonstrukci z kalibrovaných kamer.
Vypočetli jsme projektivní rekonstrukci scény a ověřili správnost výpočtu
zpětnou reprojekcí bodů. Nalezli jsme transformaci mezi skutečnou scénou a námi
vypočtenou projektivní rekonstrukcí. Ukázali jsme, že lepší výsledky při výpočtu
transformační matice lze dosáhnout výpočtem z pěti 'málo koplanárních' bodů než
pomocí přeurčené soustavy rovnic a SVD.
- 1
-
©onka M., Hlavaè V., Boyle R.,
Image Processing, Analysis, and Machine Vision,
PWS, Boston, USA, 1998
Josef Sivic
2000-05-29
![\includegraphics[height=0.4\linewidth]{fig/k15in1.eps}](img2.gif)
![\includegraphics[height=0.4\linewidth]{fig/k15in2.eps}](img3.gif)
![\begin{displaymath}{\bf u}_i^k=\left [\begin {array}{c} u_i\\ v_i\\ 1\end {array}\right ],
\end{displaymath}](img6.gif)
![]() .
[Proč je ale hodnost F právě 2?]
.
[Proč je ale hodnost F právě 2?]
![]() .
.
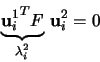
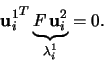
![]() a
a ![]() lze spočíst z rovnic
lze spočíst z rovnic
![\begin{displaymath}{\bf f}=\left [\begin {array}{c} f_{11}\\ \vdots\\ f_{33}\end {array}\right ],
\end{displaymath}](img19.gif)
![]() ,
kterou spočteme z osmi naměřených bodů, se od správné
matice F liší. Proto je výhodné matici A sestavit z více než osmi bodů a
hledat řešení této přeurčené soustavy metodou nejmenších čtveců (např. pomocí
SVD, viz.PVI-Úloha č.1). Hodnost spočtené matice
,
kterou spočteme z osmi naměřených bodů, se od správné
matice F liší. Proto je výhodné matici A sestavit z více než osmi bodů a
hledat řešení této přeurčené soustavy metodou nejmenších čtveců (např. pomocí
SVD, viz.PVI-Úloha č.1). Hodnost spočtené matice ![]() je obecně 3. Aby platila rovnice (1),
je potřeba hodnost
je obecně 3. Aby platila rovnice (1),
je potřeba hodnost ![]() snížit pomocí SVD na 2 (viz.PVI-Úloha č.1). Nesnížíme-li
hodnost
snížit pomocí SVD na 2 (viz.PVI-Úloha č.1). Nesnížíme-li
hodnost ![]() na 2, epipoláry se neprotnou v jednom bodě.
na 2, epipoláry se neprotnou v jednom bodě.
![]() projektivní rekonstrukce se liší od
souřadnic
projektivní rekonstrukce se liší od
souřadnic
![]() skutečné scény o lineární transformaci
H
skutečné scény o lineární transformaci
H![]() .
Výsledky zpětné projekce projektivní
rekonstrukce pomocí spočtených matic P1 a P2 jsou na obrázku 7.
.
Výsledky zpětné projekce projektivní
rekonstrukce pomocí spočtených matic P1 a P2 jsou na obrázku 7.
![\includegraphics[height=0.65\linewidth]{fig/k25prz1.eps}](img58.gif)
![\includegraphics[height=0.65\linewidth]{fig/k25prz2.eps}](img59.gif)
![]() . Geom. smysl?]
. Geom. smysl?]
![]() ,
i=1...4 koplanární, pak existuje
rovina
,
i=1...4 koplanární, pak existuje
rovina
![]() ,
,
![]() ,
taková že
,
taková že
![\includegraphics[width=0.5\linewidth]{fig/k25pr1svd.eps}](img78.gif)
![\includegraphics[width=0.5\linewidth]{fig/k25pr1.eps}](img79.gif)
![\includegraphics[width=0.5\linewidth]{fig/k25pr2.eps}](img80.gif)
![\includegraphics[width=0.5\linewidth]{fig/k25pr3.eps}](img81.gif)
![\includegraphics[width=0.5\linewidth]{fig/k25pr4.eps}](img82.gif)