Vypracoval: Pavel Konečný, Martin Šimůnek
Proveďte projektivní rekonstrukci obrazu na základě dvou vstupních obrázků.
Zde jsou zadané obrazy:
Nejprve je nutno pomocí MATLABu a modulu CORRGUI zadat korespondující body v obrazcích (bod musímí být viditelý v obou obrázcích. Tetno program sparuje souřadnice bodů a uloží je do matice. Z těchto bodů lze spočítat Fundamentální matici. Pomocí Fundamentální matice jsme v obou obrazech určili epipoly a epipolární přímky odpovídající bodům v druhém obraze. Dále jsme chytře zvolili jednu z projektivních matic a s použitím vlastností epipolární geometrii dopočítaly druhou projektivní matici. S pomocí projektivních matic jsme vypočítaly souřadnice korespondujících bodů v projektivním prostoru. Nakonec jsme zkontrolovali kvalitu projektivní rekonstrukce reprojekcí vypočítaných bodů zpět do obou obrazů.
Definujme C a C' jako stred prvni a druhe kamery. Prvni kameru umistime do
stredu souradneho systemu (ve svetovych souradnicich), tedy dostaneme T = C - C.
X je bod ve scene a u, u jsou jeho o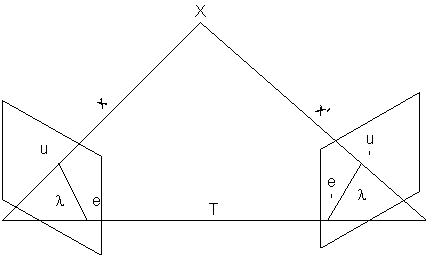
brazy j jednotlivych snimcich.
Pro výpočet matice F potřebujeme aspoň 7 korespondujících dvojic bodů.
Pro korespondující body pak platí
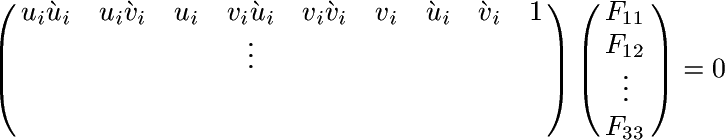
Epipolárou nazýváme takovou přímku(představuje podprostor dimenze 2), na kterou se do druhého obrazu promítá bod z prvního obrazu a tudíž ji v projektivní rovině můžeme vyjádřit pomocí doplňkového vektoru. Jelikož na epipoláře musí ležet druhý bod z korespondující dvojice, tak tento doplňkový vektor vude kolmý na vektor reprezentující bod v druhém obraze. Skalární součin kolmých vektoru reprezentujícího epipoláru a vektoru reprezentujícho bod ve druhém obraze musí být roven nule. Epipoláry v jednom obraze tudíž získám jako: uBT . F a epipoláry v druhém obraze jako: F . u'B'
Epipolem nazýváme takový bod obrazu, do kterého se promítá střed druhé kamery. Jedná se tedy o bod, který nemá v druhém obraze reprezentanta. Tudíž ve druhém obraze nemůže mít reprezentanta ani epipolára a má tedy homogenní souřadnice (0,0,0). Epipóly můžeme vypočítat z rovnic:
F . e1 = 0 a e2 . F = 0 K tomuto výpočtu opět použijeme SVD.
Dalším krokem k získání rekonstruované scény je vypočítat projekční matice, pomocí níž přepočítáme změřené body z projekční roviny do bodů rekonstruované scény.
Nejprve bylo nutno sestavit matici R obrazových bodů. Body xij jsou původní
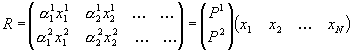
Matice P1 a P2 získáváme provedením SVD matice R. Toto lze bez zkreslení provést pouze v případě, že považujeme geometrii v obrázku za epipolární. Tedy, že rozměry předmětů v obrázku << než vzdálenost camery od předmětů. V našem případě je poměr 2:50 a dojde tedy k jemnému zkreslení celé scény.
Po zpětném spočítání souřadnic bodů získáváme
následující obrazky:
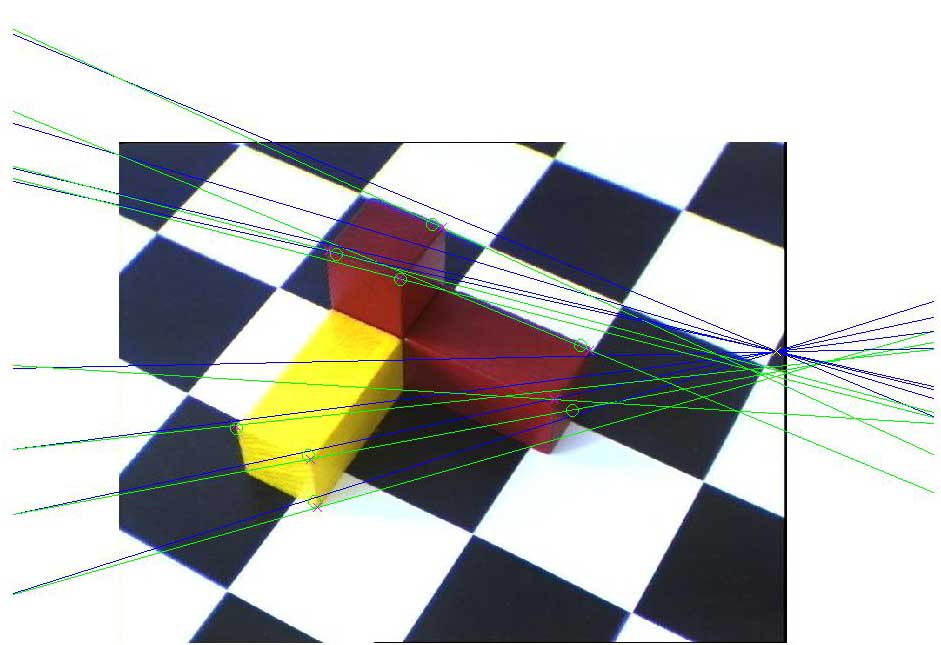
Na předcházejících obrázcích je vidět, že polohy bodů se od sebe trochu liší. Průměrná geometrická vzdálenost bodů v prvním obrazku je 11 pixelu a v druhém 9 pixelů. Tato odchylka je způsobena nepřesným určením korenspodujících bodů a metodou řešení.
Provedli jsme projektivní rekonstrukci vstupních obrázků a porovnali její výsledek s originálem. Imlementace algoritmu vedla k hlubšímu pochopení rozebíraného problému.
%-------------------------%
%
Semestralka z PVI %
%
P.Konecny %
%
M.Simunek %
%
24.5.2002 %
%-------------------------%
%----- Inicializace
dat-----------------%
M =
load_corr('kostky01-02.mat') %
N =
size(M,2);
%
%
for
J=1:N
%
H(J,1)=M(1,J)*M(3,J); %
H(J,2)=M(1,J)*M(4,J); %
H(J,3)=M(1,J);
%
H(J,4)=M(2,J)*M(3,J);
%
H(J,5)=M(2,J)*M(4,J);
%
H(J,6)=M(2,J);
%
H(J,7)=M(3,J);
%
H(J,8)=M(4,J);
%
H(J,9)=1;
%
end
%
%---------------------------------------%
%-------------------------------------------------%
%
Vypocet Fundamentalni
matice %
[U,D,V]=svd(H);
%
FF =
V(:,end);
%
F =
(reshape(FF,3,3))';
%
%
[U1,D1,V1]=svd(F);
%
D1(3,3) =
0;
%
FF =
U1*D1*V1'
%
%-------------------------------------------------%
%----------------------------%
%
Vypocet Epipolar %
E1 =
V1(:,end);
%
E1 =
E1./E1(3)
%
E0 =
U1(:,end);
%
E0 =
E0./E0(3)
%
E0'*F;
%
%----------------------------%
%----------------------------%
%
Vypocet Epipolu %
%----------------------------%
K = 1;
U2 =
[M(1:2,:);ones(1,N)*K];
U3 = [M(3:4,:);ones(1,N)*K];
L1 =
((U2'*FF)');
L2 = (FF*U3);
L3 = ((U2'*F)');
L4 = (F*U3);
for J=1:N
L1(:,J) = L1(:,J)./L1(3,J);
L2(:,J) =
L2(:,J)./L2(3,J);
L3(:,J) = L3(:,J)./L3(3,J);
L4(:,J) = L4(:,J)./L4(3,J);
end
%-----------------------------------%
% Vykresleni
epipolar do 1.obrazku
%
%-----------------------------------%
figure(1);
im =
imread('k01.jpg');
imshow(im);
hold on;
axis([-1000, 1000, -1000,
1000]);
for J=1:N
line([-1000, 1000],[
(-L2(3,J)-L2(1,J)*-1000)/L2(2,J),
(-L2(3,J)-L2(1,J)*1000)/L2(2,J)],'color','b');
line([-1000, 1000],[
(-L4(3,J)-L4(1,J)*-1000)/L4(2,J),
(-L4(3,J)-L4(1,J)*1000)/L4(2,J)],'color','g');
plot(M(1,J),M(2,J),'mX');
end
plot(E0(1),
E0(2), 'yX');
%-----------------------------------%
% Vykresleni
epipolar do 2.obrazku
%
%-----------------------------------%
figure(2);
im =
imread('k02.jpg');
imshow(im);
hold on;
axis([-1000, 1000, -1000,
1000]);
for J=1:N
line([-1000, 1000],[
(-L1(3,J)-L1(1,J)*-1000)/L1(2,J), (-L1(3,J)-L1(1,J)*1000)/L1(2,J)],'color','b'
);
line([-1000, 1000],[ (-L3(3,J)-L3(1,J)*-1000)/L3(2,J),
(-L3(3,J)-L3(1,J)*1000)/L3(2,J)],'color','g');
plot(M(3,J),M(4,J),'mX');
end
plot(E1(1), E1(2), 'yX');
%-----------------------------------%
%
Vypocet matice Rekonsturkce
%
%-----------------------------------%
R =
[U2(1:3,:);U3(1:3,:)];
[Sr,Dr,Vr] = svd(R);
Dr(5:end,5:end) = 0;
Pp =
(Sr*Dr);
Pp = Pp(:,1:4)
Xp = Vr';
Xp = Xp(1:4,:);
Xp =
Xp./(ones(4,1)*Xp(4,:))
%--- Projekcni matice --%
P1 =
Pp(1:3,:); %
P2 =
Pp(4:6,:);
%
%-----------------------%
%--------------------------------------------%
%
Zpetny vypocet a zobrazeni koren. bodu %
Body1 =
P1*Xp
%
Body2 =
P2*Xp
%
Body1 =
Body1./(ones(3,1)*Body1(3,:)) %
%
figure(1);
%
plot(Body1(1,:),
Body1(2,:),'gO');
%
Body2 =
Body2./(ones(3,1)*Body2(3,:))
%
figure(2);
%
plot(Body2(1,:),
Body2(2,:),'gO');
%
%--------------------------------------------%
%-------------------------------------%
% Prumerna chyba
na bod v pixelech %
%-------------------------------------%
Diff1 = U2-Body1;
Chyba1 =
sum(sqrt(sum(Diff1.^2,1)),2)/N
Diff2 = U3-Body2;
Chyba2 =
sum(sqrt(sum(Diff2.^2,1)),2)/N