

Daniel Sýkora (sykorad@fel.cvut.cz)
Úkolem bylo najít v následujících obrázcích epipóly a epipoláry, dále pak spočítat transformační matice obou kamer, pozice kontrolních bodů v projektivním prostoru a na závěr zjistit průměrnou chybu při zpětné reprojekci bodů do původních obrázků:


Základem epipolární geometrie je následující obrázek, který ilustruje hlavní myšlenku vedoucí k řešení problému rekonstrukce bodu ze dvou obrazů:
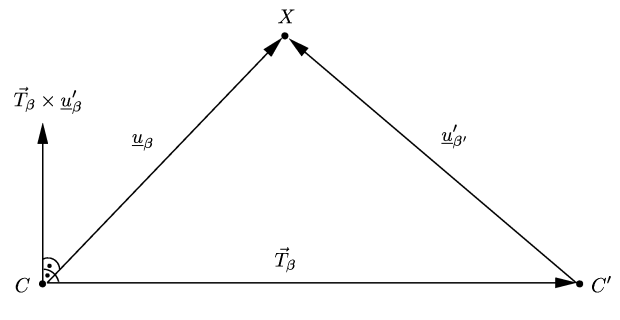
Aby se vektory u a u' protly v bodě X je nutné splnit následující vektorové rovnice:
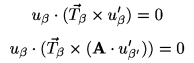
Druhá z nich navíc provádí změnu báze vektoru u' tak, abychom mohli
užít přímo souřadnice naměřené v bázi čárkovaného obrázku.
Tuto vektorovou rovnici lze dále přepsat do maticového tvaru tak, že vektorový
součin nahradíme maticí, která jej provede v rámci maticového násobení:
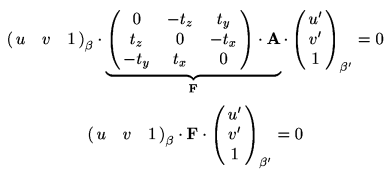
Matice vektorového součinu vynásobená transformační maticí báze čárkovaného obrázku
do obrázku nečárkovaného představuje fundamentální matici rekonstrukce bodu X.
Právě tuto matici budeme potřebovat pro zobrazení epipólů a epipolár.
Existují dvě metody, jak tuto matici získat. Uvedeme si nejprve první, která
v našem konkrétním případě dává numericky přesnější výsledky.
Vzhledem k tomu, že hodnost matice vektorového součinu je 2 a hodnost transformační
matice báze je 3, bude mít nutně i matice F hodnost 2. Matice F má
devět parametrů, z nichž jeden je díky hodnosti 2 volitelný. Bude tedy nutné naměřit
souřadnice 8 kontrolních bodů (nejlépe normované na interval <0,1>)
a sestavit následující homogenní soustavu rovnic:
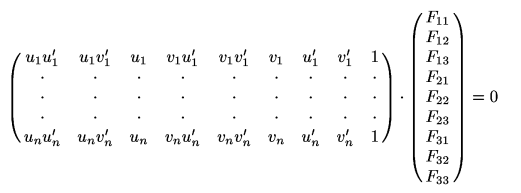
Pomocí SVD získáme fundamentální matici, kterou upravíme na hodnost 2 vynulováním prvků na diagonále matice D s indexem vyšším než 3. Pokud bychom hodnost matice F neupravili, nebudou epipoláry procházet přesně epipólem zato odchylka kontrolních bodů od epipolár bude podstatně menší. Pomocí takto upravené matice F vypočteme epipóly (pozice druhé kamery v daném obrázku) a sestrojíme epipoláry (spojnice bodů v obraze s epipólem). Platí pro ně následující vztahy:

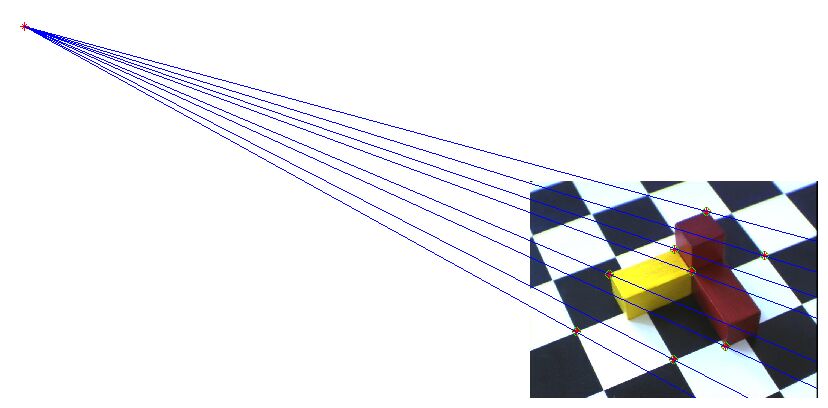
Následující dva obrázky ukazují detailně rozmístění bodů a průchody epipolár v jejich blízkosti:


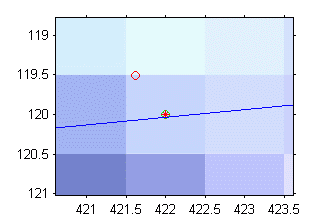
Odchylka není na první pohled patrná, protože je podstatně menší než jeden pixel. Následující grafy ukazují detail odchylky od epipoláry jednoho z vybraných bodů. Levý graf pro případ upravené hodnosti matice F a pravý bez úpravy:
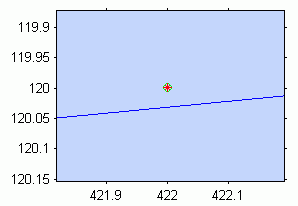
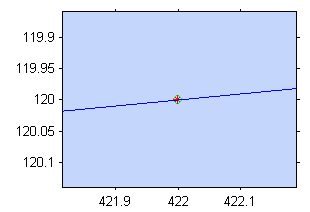
Nyní přistoupíme k rekonstrukci souřadnic kontrolních bodů v projektivním prostoru a k výpočtu transformačních matic obou kamer. Základem výpočtu bude tato soustava rovnic:
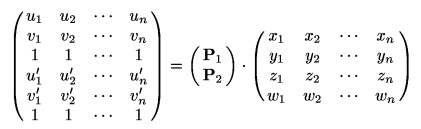
Správně bychom měli na levé straně uvést matici R, která zahrnuje ve svých koeficientech i projektivní hloubky naměřených bodů:
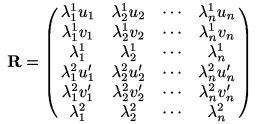
Vzhledem k tomu, že v naší úloze nepotřebujeme získat realistickou rekonstrukci zachovávající pravé úhly a topologii skutečné scény, postačí když všechny projektivní hloubky nastavíme na jedničku. Pomocí SVD pak rozložíme takto upravenou matici R na součin dvou matic:
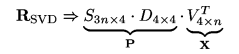
Všechny matice po výstupu z SVD omezíme tak, aby D měla rozměr 4x4, S 24x4 a V 8x4. Součinem S a D získáme matici P, ve které jsou pod sebou transformační matice nečárkované a čárkované kamery. Vlastní rekonstruované souřadnice bodů v projektivním prostoru udávají sloupce matice V. Body z matice V znormujeme a provedeme jejich zpětnou transformaci do obrázků pomocí příslušných transformačních matic. Získáme tyto dva obrázky:


Červené kroužky jsou rekonstruované a zelené s červenou hvězdičkou naklikané body. I v tomto případě nejsou odchylky příliš výrazné, přestože v několika případech přesahují i dvou-pixelovou hranici. Uvádím pro ilustraci detail chyby rekonstrukce již dříve zkoumaného bodu. Napravo od obrázku je tabulka s chybami všech rekonstruovaných bodů včetně jejich průměrné hodnoty pro oba obrázky:
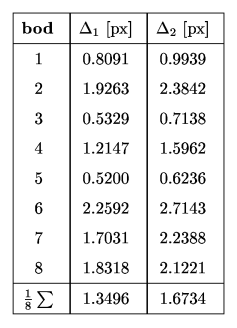
Je zajímavé, že i pomocí samotných transformačních matic obou kamer lze vypočítat fundamentální matici F, která se od již dříve vypočítané bude lišit pouze o konstantní násobek. Pro získání fundamentální matice F bude nutné jednu z transformačních matic převést na matici jednotkovou pomocí neznámé matice H. Když pak pomocí této matice ztransformujeme i matici druhé kamery, získáme sub-matici A 3x3 a vektor a reprezentující přechod od středu nečárkované ke středu čárkované kamery v bázi čárkované kamery. Budeme postupovat následovně:
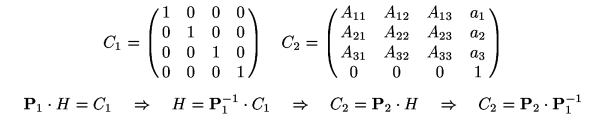
Modifikované transformační matice kamer označíme C. Převedeme matice P
na rozměr 4x4 doplněním vektoru (0 0 0 1), aby bylo možné počítat
inverzní matice, a jednoduše pak vypočteme matici H. Následně z druhé
matice C extrahujeme sub-matici A a vektor a, které dosadíme
do vztahu:
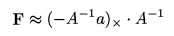
Zde znovu uplatníme konverzi vektorového součinu na maticové násobení a získáme matici F, která by měla mít přímo hodnost 2. Zobrazíme si epipoláry pomocí nově vypočtené matice F:


Výsledné epipoláry jsou téměř rovnoběžné z čehož automaticky vyplývá velká vzdálenost epipólu. Odchylky od epipolár jsou již patrné. Pro srovnání si zobrazíme jednu z nich v již dříve zkoumaném kontrolním bodě:
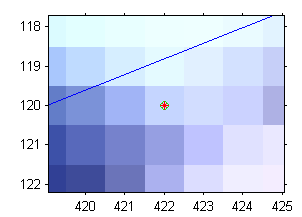
Díky normalizovaným souřadnicím naklikaných bodů bylo dosaženo poměrně dobré přesnosti ve všech uvedených výpočtech. Zajímavý je také výsledek alternativního způsobu výpočtu fundamentální matice. Zde je k dispozici matlabovský skript, který v praxi realizuje výše uvedené výpočty.