Zadání

Složte dva překrývající se snímky pořízené perspektivní kamerou tak, aby vytvořily celkový panoramatický pohled.

Obrázek 1: Vstupní snímky.

Model

Panoramatický pohled na scénu vytvoříme tak, že dané snímky promítneme do společné obrazové roviny. Pro jednoduchost budeme dále předpokládat, že snímky byly pořízeny kamerou, která se otáčela kolem svislé osy procházející jejím optickým středem C, viz obrázek 2.

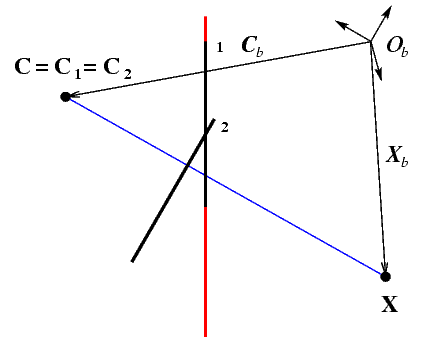Obrázek 2: Schematické znázornění pořízení jednotlivých snímků.

Pozorovaný bod X má v souřadné soustavě světa O_b zaměření X_b a optický střed kamery C má zaměření C_b. Na základě matematického modelu kamery podle [2, str. 6] potom můžeme pro oba snímky psát

	α1 ub1   =   A1 ( Xb - Cb )  ,	(1)
	α2 ub2   =   A2 ( Xb - Cb )  .	(2)

Zde  α_i  je konstanta z R \ {0},  u_bi = [ u_bi   v_bi   1 ]^T jsou homogenní souřadnice pozorovaného bodu X v obrazové rovině i-tého snímku v bázi b_i ,  A_i z R^3x3 je regulární matice přechodu od báze b k bázi b_i  a  i = 1, 2 je pořadové číslo snímku.

Protože obě kamery mají společný optický střed  C_b  a pozorují stejný bod v prostoru  X_b , dostaneme porovnáním rovnic (1) a (2) výraz

α1 A1-1ub1   =   α2 A2-1ub2  .

(3)

Volbou matice  H = A₂ A₁^-1  a konstanty  α = α₂ / α₁ , dostaneme úpravou (3) rovnici

α ub2   =   H ub1  .

(4)

Vzniklá matice H (tzv. homografie) je regulární matice z R^3x3, která popisuje korespondence všech bodů mezi dvěma obrazy.

Obrazovou rovinu výsledné panoramatické scény jsme zvolili totožnou s obrazovou rovinou prvního snímku. Hledaným vztahem je v tomto případě identita I, tj. obraz se pouze zkopíruje. Druhý snímek jsme do panoramatického obrazu transformovali pomocí homografie H. Celou situaci zachycuje obrázek 3. Zde  O_b1  a  O_b2  představují souřadné soustavy vstupních snímků.

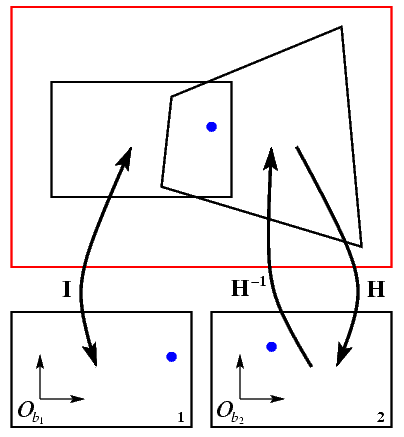Obrázek 3: Vytvoření mozaiky panoramatického pohledu.

Výpočet homografie

Homografii H lze určit na základě znalosti souřadnic několika dvojic korespondujících bodů a přímek v obou obrazech.

Výpočet homografie z korespondujících bodů

Každou dvojici korespondujících bodů označme indexem  j = 1, ... , n. Potom lze podle (4) pro každou takovou dvojici psát

αj u'j   =   H uj  ,

(5)

kde  u_j = [ u_j   v_j   1 ]^T a  u'_j = [ u'_j   v'_j   1 ]^T jsou homogenní souřadnice j-té korespondence, H je homografie a α_j je neznámá konstanta z R \ {0}.

Nechť h₁^T, h₂^T a  h₃^T jsou řádky matice H. Pro každou korespondenci s pořadovým číslem  j  tak ze vztahu (5) získáme soustavu rovnic

αj u'j	=	h1T uj  ,	(6)
αj v'j	=	h2T uj  ,	(7)
αj	=	h3T uj  .	(8)

Dosazením vztahu (8) za α_j do (6) a (7) získáme dvě lineární algebraické rovnice pro neznámé h₁, h₂ a h₃, tedy

	h3T uj u'j   =   h1T uj  ,
	h3T uj v'j   =   h2T uj  .

Pro všechny korespondence bodů ve dvou obrazech tak získáme systém 2n homogenních lineárních algebraických rovnic pro 9 neznámých, který lze přepsat do maticového tvaru

	-ujT   0 0 0   u'j ujT 0 0 0 -ujT v'j ujT :			h1 h2 h3		=   0,      j = 1, ... , n,

a který symbolicky označíme

A h   =   0 .

(9)

Protože používáme homogenní souřadnice, je homografie H v rovnici (5) určena až na skalární násobek α_j jednoznačně. Matice A má díky tomu hodnost pouze osm. K určení homografie proto musíme v matici A získat osm lineárně nezávislých řádků. Protože každá dvojice korespondujících bodů označená indexem  j dává dvě rovnice, stačí volit počet korespondencí n = 4. Tyto body nesmějí ani v jednom z obrazů ležet na přímkách.

Řešením soustavy (9) je nulový prostor matice A, který nalezneme pomocí jejího SVD rozkladu, viz [3, str. 113]. Aby byl výpočet robustní vůči chybám a šumu, je výhodné takových korespondencí použít n >> 4.

Výpočet homografie z přímek

Matici homografie H lze určit i na základě znalosti souřadnic korespondujících přímek v jednotlivých obrazech. Dá se ukázat, že přímka se v našem případě mezi dvěma obrazy transformuje podle rovnice

HT lb2   =   γ lb1  .

(10)

Zde γ je konstanta z R \ {0},  i = 1, 2 je pořadové číslo snímku,  l_bi = [ u_bi   v_bi   w_bi ]^T jsou souřadnice přímky v obrazové rovině i-tého snímku v bázi b_i  a  H z R^3x3 je homografie, která je stejná jako ve vztahu (4).

Mějme ve dvou obrazech n korespondujících přímek a jednotlivé korespondence označme indexy  j = 1, ... , n. Pro každou korespondenci pak můžeme podle (10) psát

γj lj   =   HT l'j  ,

(11)

kde   l_j   =   [ u_j   v_j   w_j ]^T  a  l'_j   =   [ u'_j   v'_j   w'_j ]^T jsou souřadnice přímek v příslušných bázích, H je homografie a γ_j je neznámá konstanta z R \ {0}.

Když sloupce matice H označíme q₁, q₂ a  q₃, pak rozepsáním (11) získáme pro každou korespondenci soustavu rovnic

γj uj	=	q1T l'j  ,
γj vj	=	q2T l'j  ,
γj wj	=	q3T l'j  .

Abychom vyeliminovali neznámou konstantu γ_j , podělíme vzájemně každé dvě rovnice a dostaneme

( γj uj ) / ( γj wj )	=	( q1T l'j ) / ( q3T l'j )  ,
( γj vj ) / ( γj wj )	=	( q2T l'j ) / ( q3T l'j )  ,
( γj uj ) / ( γj vj )	=	( q1T l'j ) / ( q2T l'j )  .

Odtud úpravou získáme ekvivalentní soustavu tří homogenních lineárních algrebraických rovnic pro neznámé q₁, q₂ a  q₃, tedy

-wj q1T l'j   +   uj q3T l'j   =   0  ,

-wj q2T l'j   +   vj q3T l'j   =   0  ,

-vj q1T l'j   +   uj q2T l'j   =   0  .

Pro všechny korespondence přímek dále sestavíme systém 3n homogenních lineárních algebraických rovnic pro 9 neznámých, který přepíšeme do maticového tvaru

	-wj l'jT   0 0 0   uj l'jT   0 0 0   -wj l'jT vj l'jT -vj l'jT uj l'jT   0 0 0			q1 q2 q3		=   0,      j = 1, ... , n,
	:

a který pro jednoduchost zapíšeme

B q   =   0  .

(12)

Homografie H v rovnici (11) je určena, podobně jako tomu bylo ve vztahu (5), až na skalární násobek γ_j jednoznačně. Matice B má díky tomu hodnost pouze osm. Kγurčení homografie H z přímek proto potřebujeme v matici B získat osm lineárně nezávislých řádků. Protože každá dvojice korespondujících přímek označená indexem  j dává dva lineárně nezávislé řádky matice B, stačí volit počet korespondencí n = 4. Tyto přímky musí v obou obrazech ležet v obecné poloze.

Řešením soustavy (12) je nulový prostor matice B, který nalezneme pomocí jejího SVD rozkladu, viz [3, str. 113]. Aby byl výpočet robustní vůči chybám a šumu, je výhodné takových korespondencí použít n >> 4.

Výpočet homografie z bodů a přímek

Homografii H lze určit i z krespondencí bodů a přímek zároveň. Podobně, jako tomu bylo v rovnicích (9) a (12), lze i pro tento případ sestavit soustavu homogenních lineárních algebraických rovnic a oba předchozí postupy tak sloučit. Tímto problémem jsme se však dále nezabývali.

Normalizace dat

Abychom při výpočtu homografie H minimalizovali numerické chyby, musí být matice A, resp. B dobře podmíněna, viz [3, str. 111]. Je proto výhodné každý ze souborů vstupních souřadnic  u_j  a  u'_j, resp.  l_j  a  l'_j  jednotlivých korespondencí normovat tak, aby výsledné soubory  u_j a  u'_j , resp.  l_j a  l'_j , ze kterých budeme matici A, resp. B, sestavovat, měly střední hodnotu  mean(X)  =  μ_X   =  [ 0   0   1 ]^T  a rozptyl  var(X)  =  σ_X²  =  [ 1   1   0 ]^T, viz [4, str. 466].

Normované souřadnice  X_j = [ x_j   y_j   1 ]^T pro sestavení matice A, resp. B jsme pro všechny korespondence  j = 1, ... , n  vypočetli podle

Xj   =   NX Xj  ,

(13)

kde  X_j = [ x_j   y_j   1 ]^T jsou původní souřadnice a matice N_X byla určena jako

NX  =		1 / σx 0 -μx / σx 0 1 / σy -μy / σy 0 0 1		.

Zde  μ_x  a  μ_y  jsou střední hodnoty a  σ_x  a  σ_y  jsou rozptyly ve složkách  x  a  y  původních souřadnic.

Vztah korespondence všech bodů v obou obrazech podle (5) potom přejde do tvaru

αj u'j   =   H uj   =   Nu'-1 Hu'u Nu uj  ,

(14)

kde  N_u  a  N_u'  jsou normalizační matice,  H_u'u  je vypočtena z normovaných dat řešením soustavy rovnic (9) a homografie H   =   N_u'^-1 H_u'u N_u .

Podobně i vztah korespondence všech přímek podle (11) přejde do tvaru

γj lj   =   HT l'j   =   Nl-1 Hll'T Nl' l'j  .

(15)

Zde  N_l  a  N_l'  jsou normalizační matice,  H_ll'  je vypočtena z normovaných dat řešením soustavy rovnic (12) a homografie H^T   =   N_l^-1 H_ll'^T N_l' .

Výsledky

Korespondence

Korespondující body v obou snímcích jsme určili v prostředí MATLAB 5.3 pomocí programu CORRGUI. Body byly voleny tak, aby pokrývaly co nejvetší plochu překrývajících se částí obou obrazů. Pro výpočet homografie jsme použili osm bodů, viz obrázek č. 4.

Obrázek 4: Vyznačení korespondujících bodů v jednotlivých obrazech.

Souřadnice přímek v obrazech jsme získali z automaticky vygenerovaných souborů, které byly součástí zadání. Pro výpočet homografie H jsme jich vybrali osmnáct tak, aby byly rozmístěny na co největší ploše v překrývajících se částech obou obrazů, viz obrázek č. 5. Při volbě menšího počtu korespondencí jsme již nedostávali dobré výsledky.

Obrázek 5: Vyznačení korespondujících přímek v jednotlivých obrazech.

Homografie určená z bodů

Výpočtem podle (9) jsme bez normalizace souřadnic bodů získali homografii

H  =		0,6073 0,0001 317,6037 -0,1523 0,8977 16,2641 -0,0007 -0,0000 1,0000		,

kde podmíněnost matice A byla  χ(A) = 46667323,6. Normalizací dat podle (13) byla podmíněnost  χ(A) = 268,6  a homografie

H  =		0,6304 -0,0037 317,4196 -0,1434 0,9000 15,1983 -0,0007 -0,0000 1,0000		.

Homografie určená z přímek

Bez normalizace souřadnic přímek jsme výpočtem podle (12) získali homografii

H  =		0,5839 -0,2310 346,7181 -0,1192 0,6962 43,8550 -0,0005 -0,0004 1,0000		,

kde podmíněnost matice B byla  χ(B) = 34547129. Normalizací podle (13) jsme dostali homografii

H  =		0,6156 -0,0664 323,9327 -0,1355 0,8523 20,2996 -0,0006 -0,0002 1,0000		.

Podmíněnost matice B byla v tomto případě  χ(B) = 318,5.

Mozaiky panoramatu

Složené mozaiky panoramatu Karlova mostu můžeme vidět na obrázcích č. 6 až 9 vlevo. Pro aproximaci hodnot jasové funkce byla použita bilineární interpolace, viz [5, str. 140]. Na obrázcích vpravo jsou pak znázorněny rozdílové snímky překrývajících se částí obou obrazů. Čím tmavší odstín je použit, tím větší je rozdíl mezi skládanými snímky (bílá barva odpovídá nulovému rozdílu).

Obrázek 6: Panorama Karlova mostu; homografie byla určena z původních souřadnic korespondujících bodů.

Obrázek 7: Panorama Karlova mostu; homografie byla určena z normovaných souřadnic korespondujících bodů.

Obrázek 8: Panorama Karlova mostu; homografie byla určena z původních souřadnic korespondujících přímek.

Obrázek 9: Panorama Karlova mostu; homografie byla určena z normovaných souřadnic korespondujících přímek.

Závěr

Cílem úlohy bylo vytvořit panoramatatický obraz složený ze 2 snímků. Ty byly pořízeny kamerou, která se otáčela kolem svého optického středu.

Algoritmus jsme implementovali v prostředí MATLAB 5.3. Pro sestavení panoramatu jsme využili homografie, která byla v jednom případě určena z osmi korespondujících bodů a ve druhém z osmnácti korespondujících přímek v jednotlivých obrazech. Pro výpočet byly použity původní i normované souřadnice. K aproximaci hodnot jasové funkce při transformaci obrazu byla použita bilineární interpolace.

Dosažené výsledky jsme porovnali na základě rozdílových snímků překrývajících se oblastí obrazů. Nejlepší výsledky byly dosaženy pomocí homografie vypočtené z normovaných souřadnic korespondujících bodů. Nejhorší výsledky pak dávala homografie vypočtená z původních souřadnic přímek.

[1] T. Pajdla: Přednášky z PVI 2003;  http://cmp.felk.cvut.cz/cmp/courses/pvi2003/LectureNotesPVI2003/, přístupné 8.6.2003.
[2] J. Šochman, T. Pajdla: Matematický model kamery v afinním prostoru. Výzkumná zpráva TR-2002-11. CMP FEL ČVUT, Praha, 2002, 7 pp.
[3] E. Krajník: Maticový počet. Skripta, vydavatelství ČVUT, Praha, 2000.
[4] M. Šonka, V. Hlaváč, R. Boyle: Image processing, analysis and machine vision. 2nd ed., PWS, Boston, 1998.
[5] V. Hlaváč, M. Sedláček: Zpracování signálů a obrazů. Skripta, vydavatelství ČVUT, Praha, 2000.