The EM Algorithm for Nick Carter

Famous investigator Nick Carter got into troubles while solving a case of mysterious disappearance of lady Thun's dog. The only clue he was able to obtain was a set of photographs of the likely villain. Unfortunatelly, the photographs are of so low quality, that they are almost unreadable.

How is Nick now missing his 33RPZ seminars, which he was light-headedly skipping during his studies. Well, it's now too late to feel sorry about it. On his own, he is unable to exploit the photographs he have and successfully solve the case. Fortunatelly, his old friend, inspector Kidney, got a bright idea, and told him about you, our talented students.

So there we have Nick, in a dire need of your help. Can you help him to reveal the true identity of the villain?

Figure 1. Nick Carter pondering the EM algorithm

The clues

So the unfortunate Nick has m corrupted images of H_img x W_img pixels (Figure 2). He knows, that each image depicts the face of the villain. He suspects, that the faces do not occupy whole images - the image size of a face is only H_img x w pixels. I.e. a face spans whole height of the image, but is narrower. Thus, only the horizontal position of the face varies in the images (i.e. we can assume that horizontal position k is the only unknown). We also know that backround of the images (i.e. the image area outside the face itself) is constant - has constant intensity b. See figure 3. The images are very noisy (assume gaussian noise distribution here).

Figure 2. One of the Nick's images

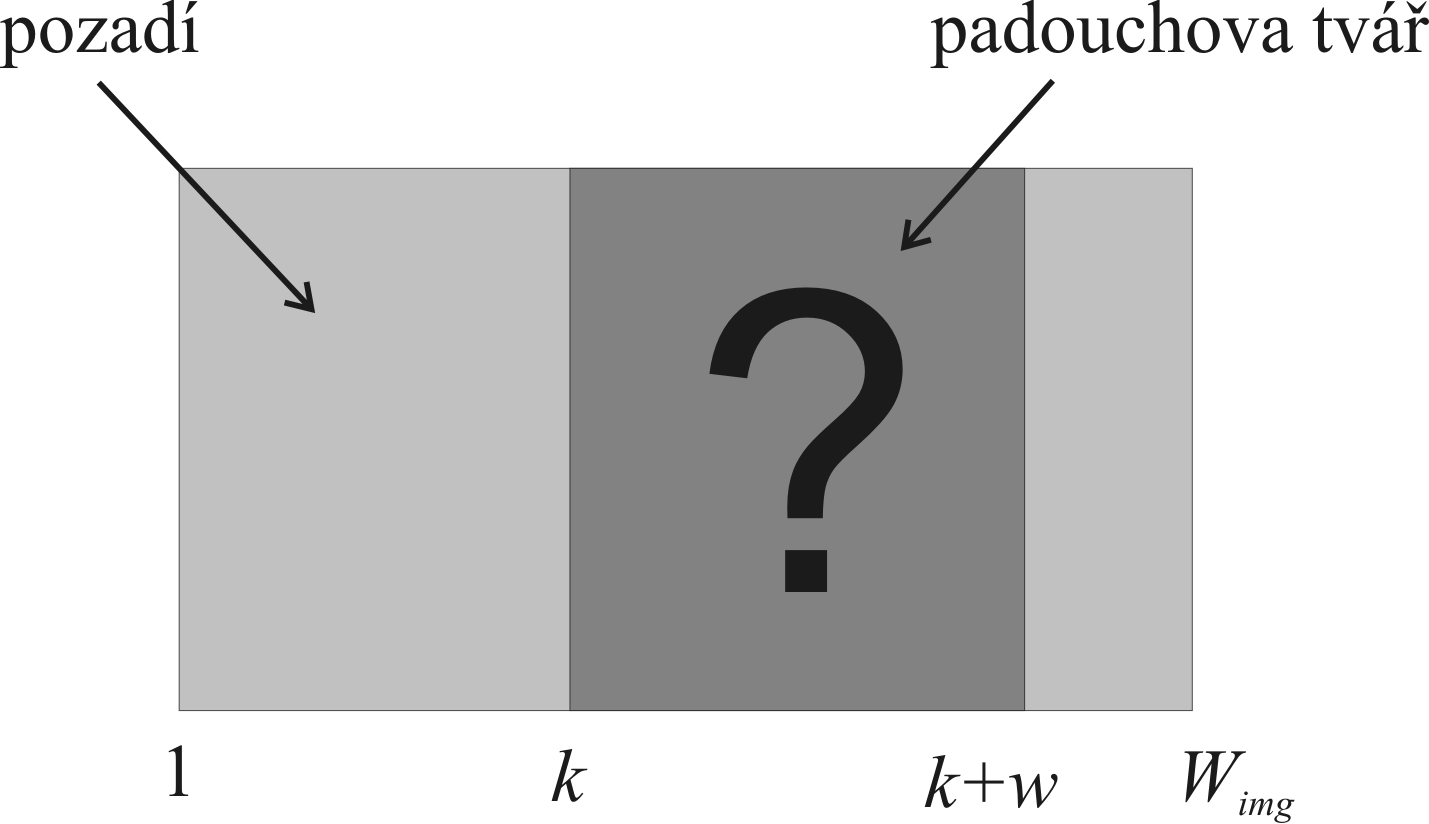
Figure 3. Image composition. The face is at an unknown horizontal position k.

The stochastic model

We have a set of m images {X₁, X₂, ... , X_m}, of H_img × W_imgpixels. X_is are the images, each has n = H_img * W_imgpixels. In each image there is the villain's face F at position k. The face dimension is H_img x w pixels, pixels outside the face have constant intensity b. Each pixel X_i(r,c), i.e. pixel in i-th image at position (r, c), is observed with a gaussian noise N (0,σ). Therefore, the probability of observing value X_i(r,c), assuming face at position k_i, is:

for background pixels (for c: 1 <= c < k_i OR k_i+w <= c <=W_img ):

P(x_i(r,c) | k_i) = N(b, σ)
for face pixels (i.e. for c: k_i <= c < k_i+w ):

P(x_i(r,c) | k_i) = N(F(r,c-k_i+1), σ) .

The probability of observing image X_i, assuming face at position k_i, can be written as a product over all pixels:

P( X_i | k_i ) = Π_r Π_c P( x_i(r,c) | k_i) .

The probability of observing the set of all m images P( {X₁,...,X_m} ) is

P( {X₁,...,X_m} ) = Π_i P( X_i) = Π_i Σ_k P( X_i , k) = Π_i Σ_k P(k) P( X_i | k) .

Taking the logarithm, we obtain the likelihood of the image set: L = log P( {X₁,...,X_m} ) .

As Nick Carter correctly guessed, the most likely estimate of the villain's face F can be obtained using the EM algorithm. Hidden parameters are here the face positions k_i , i=1,..,m in the images.

EM Formulation

The EM algorithm will be used for finding the Maximal Likelihood (ML)-estimate of parameters F, b, σ

(F, b, σ) = argmax P({X₁,...,X_m}|F, b, σ).

The hidden parameters are the face positions k_i.

The EM algorithm iteratively executes in two steps, E-step and M-step:

The E-step:
In the E-step, coefficients α(k,i) are computed for current estimates of F, b, σ:

α(k,i) = P(k) * P(X_i | k) / Σ_k [ P(k) * P(X_i | k) ] ,

where k = 1,...,W_img-w+1, i = 1,...,m.
The coefficients α(k,i) represent estimates of probability P(k_i|X_i). In other words, here we estimate the probability, that i-th image contains the face F at position k_i. The probability is evaluated for all images and for all possible positions.
The M-step:
In the M-step, parameters P(k), F, b, and σ are estimated (by maximising the lower bound of the likelihood) for current estimates of α(k,i). The probability P(k) is computed as the average of α(k,i) over all images i.

P(k) = Σ_i α(k,i) / m ,
where k = 1, ..., W_img - w + 1, and the sum goes over i = 1, ..., m. The remaining parameters F, b, σ are estimated by maximising

(F, b, σ) = argmax Σ_i Σ_k α(k,i) * log P(X_i | k, F, b, σ) , (1)
k = 1, ..., W_img- w + 1, and the sum again goes over i = 1, ..., m. The equations for F, b, σ are obtained by setting respective partial derivations of eq. (1) to zero. We get

F = [ Σ_i Σ_k α(k,i) * X_i (:, k:k+w-1) ] / m
b = [ Σ_i Σ_k α(k,i) * S(k,i) ] / [ m * (n-H_img*w) ] ,
σ² = [ Σ_i Σ_k α(k,i) * ( A(k,i) + B(k,i) ) ] / (m*n) ,

where S( k,i) = Σ_r Σ_c X_i( r,c) , r=1,..., H_img , c=[1:k-1, k+w:W_img]
A(k,i) = Σ_r Σ_c [ X_i ( r,k+c-1) - F(r,c) ]² , r=1,...,H_img , c=1,...,w
B( k,i) = Σ_r Σ_c [ X_i( r,c) - b ]² , r=1,..., H_img , c=[1:k-1, k+w:W_img]

( Try to derive the equation for b. Set the partial derivation of eq. (1) to zero, and express b. )

The tasks

Go through the EM algorithm.
Try to derive the equation for b (the background intensity) in the M-step.
Use the EM-algorithm to obtain the maximally likely estimate of the villain's face F. In each iteration, display the actual estimate of F along with the likelihood of the estimate. The input images can be downloaded here from image_data.mat. The datafile contains 500 images of 45x60 pixels. The face width w is expected to be 36 pixels. Compute the estimate for
increasing m = 10,100,500.
In the first 10 images, mark the face position k_i which you have found, k_i = argmax _{k_i} P( k_i | X_i).

Figure 4. The mostlikely face position k₁in the first image.

Hint

In the E-step, it is reccommended first to sum up all the exponents of the gaussian distributions, which occur in the products. Also, to avoid rounding errors in the exp function, it is reccommended, before the division takes place, to multiply both the numerator and the denumerator of the fraction by a large constant (i.e. by adding a large number to the exponents).

References

[1] Expectation-maximization algorithm (Wikipedia).
[2] Michail I. Schlesinger, Vaclav Hlavac. Ten Lectures on Statistical and Structural Pattern Recognition. Kluwer Academic Publishers, 2002.

Created by Martin Urban, last update 18.7.2011