Neymanova-Pearsonova úloha

Jste kapitánem obchodní lodi a plavíte se Karibským mořem. Cesta by měla být bezpečná, již mnoho let zde nikdo pirátksou loď nespatřil. Přesto máte špatné tušení a od rána do večera pečlivě sledujete obzor. Na obzoru pozorujete mnoho neznámých lodí. Co kdyby některá přeci jen patřila obávanému Pirátovi z Karibiku?

obr.1 Obchodní loď obr.2 Pirátská loď


Abychom Vám úlohu zjednodušili, předpokládejme, že k rozlišení obchodní a pirátské plachetnice používáte jednorozměrné diskrétní měření

  x = round( (průměrná intensita levé poloviny obrázku) - (průměrná intensita pravé poloviny obrázku) )

Z námořní příručky znáte rozložení zmíněné veličiny mezi obchodními loděmi P(x|1) a pirátskými loděmi P(x|2). Jaká je apriorní pravděpodobnost setkání s piráty P(2) ale vůbec netušíte.

Vaším cílem je nalézt na základě známých diskrétních rozložení P(x|1) a P(x|2) takovou rozhodovací strategii, která bude minimalizovat pravděpodobnost falešného poplachu za předpokladu, že pravděpodobnost přehlédnutí pirátské karavely nepřekročí nějakou rozumnou hranici ε.

Pokud strategii klasifujicí x do třídy 1 a 2 zapíšeme pomocí funkce q(x) takové, že

q(x) = 0 ... pokud x klasifikuji do třídy 1 (obchodní lodě)
q(x) = 1 ... pokud x klasifikuji do třídy 2 (pirátské lodě),

potom podmíněnou pravděpodobnost falešného poplachu mohu vyjádřit jako Sum_x q(x) P(x|1) a podmíněnou pravěpodobnost přehlédnutí pirátské lodi jako Sum_x [1-q(x)] P(x|2). (V sumách sčítám přes diskrétní obor hodnot x).


Neyman-Pearson úlohu potom zapíši jako hledání strategie q(x):

q = argmin Sum_x q(x) P(x|1), za podmínky

Sum_x [1-q(x)] P(x|2) <= ε.

Zadání

  1. Stáhněte a nahrajte si do Matlabu soubor neyman-pearson-pxi.mat, který obsahuje diskrétní distribuce P(x|1), P(x|2).

    Obsah souboru:
    Px1 - 1x62, diskrétní distribuce P(x|1)
    Px2 - 1x62, diskrétní distribuce P(x|2)
    X - 1x62, množina X, množina hodnot veličiny x; X = {-43,-42,...,18}

  2. Vykreslete distribuce P(x|1) a P(x|2) do jednoho obrázku.
    Pxi
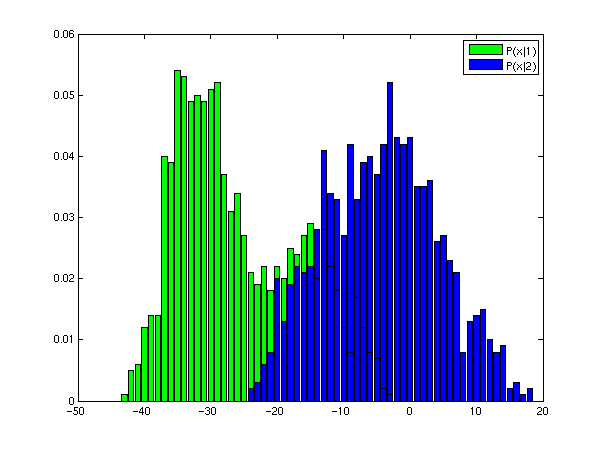
    obr.3. Očekávaný výsledek.


  3. Zapište úlohu hledání optimální strategie q(x) jako úlohu lineárního programování.
  4. Pro zvolené ε nalezněte optimální strategii. K vyřešení úlohy lineárního programování použijte matlabovskou funkci

    α = LINPROG(f,A,b,Aeq,beq,LB,UB),

    která minimalizuje f' * α za podmínek A * α <= b, Aeq * α = beq, LB <= α <= UB.
  5. Nalezenou optimální strategii znázorněte do obrázku s distribucemi P(x|1) a P(x|2).
    Pxi
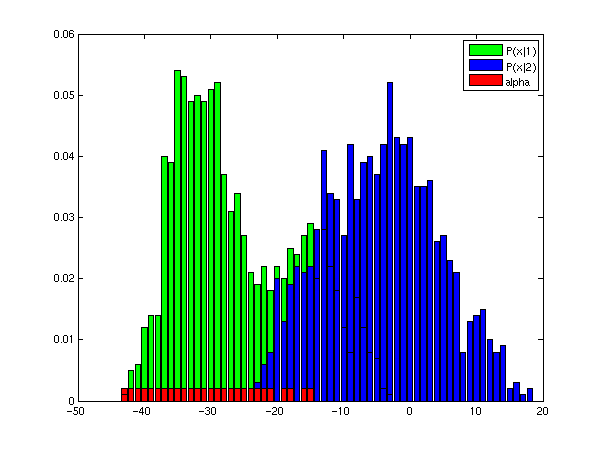
    obr.4. Ukázka možného výsledku. Červená políčka označují biny, které klasifikuji do třídy 1.


  6. Pro optimální strategii vyčíslete pravděpodobnost falešného poplachu a pravděpodobnost přehlédnutí pirátské lodi.
  7. Stáhněte si soubor neyman-pearson-images.mat, který obsahuje obrázky pozorovaných plachetnic.

    Obsah souboru:
    images - 100x100x110, 110 obrázků pozorovaných lodí
    labels - 1x110, vektor se správnou klasifikací

    Klasifikujte obrázky pomocí vypočtené optimální strategie. Porovnáním se skutečnou klasifikací (vektor labels) spočtěte empirické chyby (tj. procento falešných poplachů a procento přehlédnutých pirátských lodí.) Empirické chyby porovnejte se střední hodnotou chyb z bodu 6.
  8. Body 4-7 zopakujte pro několik různých hodnot ε. Vypočtená očekávání chyb a změřené empirické chyby zapište do tabulky.

Bonusová úloha

(pro zdatné studenty)
Vyřešte body 3-8, tentokrát ale jako Waldovu úlohu.

Doporučená literatura

Created by Martin Urban,  last update 22.10.2007