Stable monotonic matching is stable and preserves ordering.
Confidently stable matching uses confidence intervals instead of single-valued correlation values.
For exact definition and properties see the paper.
|
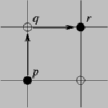
Matching M (full circles) is stable if each match p from
M has no other competitors q besides those that have a
competitor r from M. Match q is a competitor to
a match p if they cannot be both members of M (due to
uniqueness or ordering constraints, for instance) and the
correlation of q is greater than that of p. Obviously,
the q would be a better match candidate than p on
account of its correlation value alone.
Stable monotonic matching is stable and preserves ordering. Confidently stable matching uses confidence intervals instead of single-valued correlation values. For exact definition and properties see the paper. | 
|
| Radim Sara | Last modified: Sun Sep 16 17:58:28 CEST 2001 |