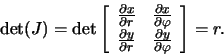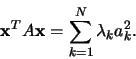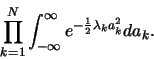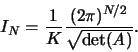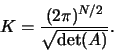Gaussův integrál - Řešení
Vyřešíme nejprve druhou mocninu integrálu
Provedeme substituci do polárních souřadnic
Determinant Jakobiánu transformace je
Čili
 .
Po provedení substituce dostaneme
.
Po provedení substituce dostaneme
Provedeme ještě jednou substituci
počítáme tedy integrál
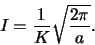 |
(1) |
Potřebujeme vyjádřit 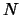 -rozměrný integrál jako součin
-rozměrný integrál jako součin 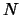 jednorozměrných integrálů. Substituujeme
jednorozměrných integrálů. Substituujeme 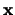 pomocí lineární
kombinace vlastních vekorů matice
pomocí lineární
kombinace vlastních vekorů matice 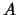 .
.
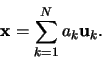 |
(2) |
Jelikož 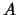 je symetrická reálná pak i
je symetrická reálná pak i  jsou reálná a
existuje ortonormální báze vlastních vektorů
jsou reálná a
existuje ortonormální báze vlastních vektorů 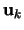 ,
podrobnosti
viz [1]. Existuje reálná ortonormální matice
,
podrobnosti
viz [1]. Existuje reálná ortonormální matice 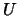 taková, že platí
taková, že platí
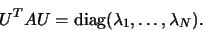 |
(3) |
Za předpokladu ortonormality vlastních vektorů,
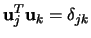 ,
platí pro determinant jakobiánu transformace
(2)
,
platí pro determinant jakobiánu transformace
(2) 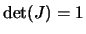 .
Připomeňme, že platí
.
Připomeňme, že platí
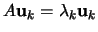 ,
kde
,
kde  jsou příslušná vlastní čísla
matice
jsou příslušná vlastní čísla
matice 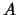 .
Pak platí
.
Pak platí
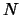 -rozměrný integrál přepíšeme na součin
-rozměrný integrál přepíšeme na součin
Tento jednorozmzěrný integrál jsme již vyřešili v předchozí
kapitole. Doplňme ještě, že z rovnice (3) vyplývá,
že součin vlastních čísel je roven determinantu matice 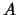 .
S použitím
výsledku (1) platí
.
S použitím
výsledku (1) platí
Z požadavku 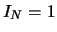 tedy
tedy
- 1
-
Gene H. Golub and Charles F. van Loan.
Matrix Computation.
The Johns Hopkins University Press, second edition, 1989.
1999-04-26