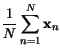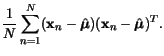Odhad parametrů
Tomáš Svoboda
Předpokládáme, že tvar hustoty rozdělení je znám 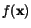 .
Na
základě pozorovaných dat se snažíme odhadnout parametry. Podrobnější
odvození může čtenář najít v knize [1] nebo
[2].
.
Na
základě pozorovaných dat se snažíme odhadnout parametry. Podrobnější
odvození může čtenář najít v knize [1] nebo
[2].
Uvažujme hustotu 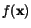 zavisící na vektoru parametrů
zavisící na vektoru parametrů
![$\mbox{\boldmath$\theta$\unboldmath }=[\theta_1, \dots, \theta_M]^T$](img2.gif) .
Pro jednoduchost nyní zanedbejme označení příslušnosti ke třídě.
Stejná úvaha platí pro všechny třídy. Pro vyjádření závislosti hustoty
na paramtrech, zavedeme podmíněnou hustotu
.
Pro jednoduchost nyní zanedbejme označení příslušnosti ke třídě.
Stejná úvaha platí pro všechny třídy. Pro vyjádření závislosti hustoty
na paramtrech, zavedeme podmíněnou hustotu
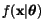 .
Z trénovací množiny
máme
.
Z trénovací množiny
máme 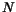 vektorů
vektorů
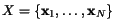 .
Za předpokladu, že
tyto vzorky byly vybrány náhodně, je jejich sdružená hutota rovna
součinu jednotlivých hustot.
.
Za předpokladu, že
tyto vzorky byly vybrány náhodně, je jejich sdružená hutota rovna
součinu jednotlivých hustot.
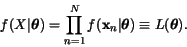 |
(1) |
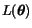 je funkce
je funkce
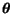 pro dané
pro dané 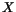 ,
nazýváme ji věrohodnost parametrů. Čili maximálně věrohodný odhad parametrů
bude takový, jenž maximalizuje hodnotu věrohodnosti, rovnice
(1) V praxi je mnohem snazší minimalizovat funkci
,
nazýváme ji věrohodnost parametrů. Čili maximálně věrohodný odhad parametrů
bude takový, jenž maximalizuje hodnotu věrohodnosti, rovnice
(1) V praxi je mnohem snazší minimalizovat funkci
Pro normální rozdělení můžeme odvodit nejvěrohodnější odhad střední
hodnoty a kovarianční matice
- 1
-
Christopher M. Bishop.
Neutral Networks for Pattern Recognition.
Clarendon Press, Oxford, Great Britain, 3th edition, 1997.
- 2
-
Athanasios Papoulis.
Probability and Statistics.
Prentice-Hall, 1990.
Tomas Svoboda
2000-03-23
![]() .
Na
základě pozorovaných dat se snažíme odhadnout parametry. Podrobnější
odvození může čtenář najít v knize [1] nebo
[2].
.
Na
základě pozorovaných dat se snažíme odhadnout parametry. Podrobnější
odvození může čtenář najít v knize [1] nebo
[2].