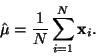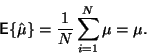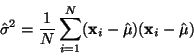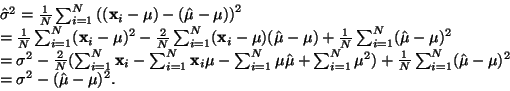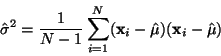Random Samples
Tomáš Svoboda
Abstract:
Pomocný text objasňující základy teorie náhodných vzorků (random
samples). Především odhad střední hodnoty a rozptylu. Vysvětelna je
momentová funkce (moment generating) funkce a odvození jednotlivých
momentů.
Moment  -tého řádu je definován
-tého řádu je definován
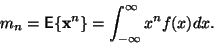 |
(1) |
Centrální moment  -tého řádu
-tého řádu
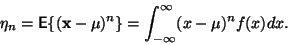 |
(2) |
Moment prvního řádu označujeme jako střední hodnotu 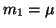 .
Druhý centrální moment označujeme jako rozptyl
.
Druhý centrální moment označujeme jako rozptyl
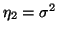 .
Odmocninu
.
Odmocninu
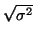 nazýváme standardní
odhylkou. Rozptyl lze spočítat z prvního a druhého momentu.
nazýváme standardní
odhylkou. Rozptyl lze spočítat z prvního a druhého momentu.
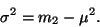 |
(3) |
Důkaz:
Odvození je převzato a upraveno z knihy [1]. Momentová
funkce náhodné veličiny 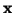 je definována jako střední hodnota
funkce
je definována jako střední hodnota
funkce
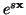 .
Funkci označíme
.
Funkci označíme 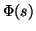 a je definována pro
všechna
a je definována pro
všechna 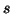 pro která
pro která
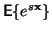 .
.
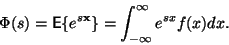 |
(4) |
Tuto funkci s výhodou využijeme při transformaci náhodných veličin.
Buď
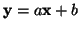 náhodná veličina. Její momentová funkce je
rovna:
náhodná veličina. Její momentová funkce je
rovna:
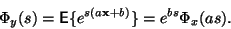 |
(5) |
Buď 
 -tý moment náhodné veličiny.
-tý moment náhodné veličiny.
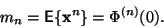 |
(6) |
Důkaz:  diferencováním (4) podle
diferencováním (4) podle 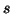 vypočteme
vypočteme
jelikož 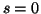 ,
tato rovnice je přesně rovnice (1).
,
tato rovnice je přesně rovnice (1).
Buď
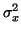 rozptyl a
rozptyl a 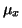 střední hodnota náhodné veličiny
střední hodnota náhodné veličiny
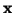 .
Definujeme náhodnou veličinu
.
Definujeme náhodnou veličinu 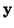 jako
jako
Nyní chceme spočitat
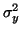 a
a  ze znalosti charakteristik
náhodné veličiny
ze znalosti charakteristik
náhodné veličiny 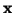 .
Známe vztah pro momentovou funkci
transformované veličiny (5). Derivujeme podle
.
Známe vztah pro momentovou funkci
transformované veličiny (5). Derivujeme podle 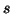
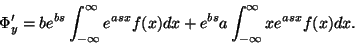 |
(7) |
po dosazení 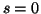 ,
,
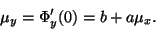 |
(8) |
Derivací rovnice (7) získáme
připomeňme, že platí
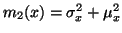 ,
viz rovnice (3). Dosazením obdržíme
,
viz rovnice (3). Dosazením obdržíme
Rozptyl veličiny 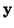 je tedy roven
je tedy roven
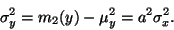 |
(9) |
Výše uvedené vztahy lze samozřejmě použít i ve vícedimenzionálním
problému. Mějme 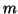 -rozměrnou náhodnou veličinu y,
-rozměrnou náhodnou veličinu y,  -rozměrnou
x a transformační matici
-rozměrnou
x a transformační matici 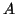 o rozměru
o rozměru 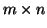 a
a 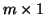 vektor b.
vektor b.
Rovnice (8) se změní na
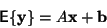 |
(10) |
a rovnice (9) bude
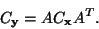 |
(11) |
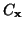 je
je 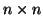 kovarianční matice x a
kovarianční matice x a 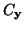 je
je
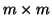 kovarianční matice vektoru y.
kovarianční matice vektoru y.
Náhodné vzorky definujeme jako sekvenci nevzájem nezávislých náhodných
veličin se stejným rozdělením (v anglické literatuře i.i.d -
independent and identically distributed).
Aritmetickému průměru
 |
(12) |
vzorků 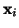 se říká střední hodnota náhodných vzorků.
Uvědomme si, že
se říká střední hodnota náhodných vzorků.
Uvědomme si, že
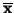 je také náhodná veličina. Připomeňme,
že vzorky
je také náhodná veličina. Připomeňme,
že vzorky 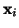 mají stejnou střední hodnotu a rozptyl. S
použitím rovnic (10) a
(11) vypočteme střední hodnotu
mají stejnou střední hodnotu a rozptyl. S
použitím rovnic (10) a
(11) vypočteme střední hodnotu
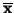
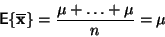 |
(13) |
pro rozptyl pak platí
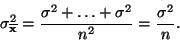 |
(14) |
Buď 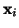 náhodné vzorky z rozdělení, jehož tvar známe, ale
neznáme jeho parametry. Předokládejme náhodné rozdělení. Odhady budeme
značit se stříškou,
náhodné vzorky z rozdělení, jehož tvar známe, ale
neznáme jeho parametry. Předokládejme náhodné rozdělení. Odhady budeme
značit se stříškou,  je tedy odhad střední hodnoty
je tedy odhad střední hodnoty 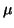 a
a
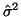 je odhad rozptylu
je odhad rozptylu 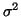 .
Metodou maximální
věrohodnosti získáme následující odhady parametrů. Pro odhad střední
hodnoty aritmetický průměr
.
Metodou maximální
věrohodnosti získáme následující odhady parametrů. Pro odhad střední
hodnoty aritmetický průměr
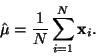 |
(15) |
Střední hodnota odhadu je (viz předchozí podkapitola)
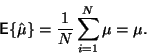 |
(16) |
Odhad střední hodnoty je tedy nevychýlený. Pro odhad rozptylu:
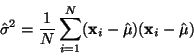 |
(17) |
Ukážeme ale, že tento odhad je vychýleným odhadem skutečného
rozptylu 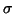 .
.
Střední hodnota odhadu rozptylu je tedy
S použitím vztahu pro rozptyl střední hodnoty (14)
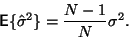 |
(18) |
Je zřejmé, že pro větší hodnoty 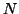 je vychýlení zanedbatelné. Je
třeba si uvědomit, že vychýlení je z důvodu použití odhadu střední
hodnoty
je vychýlení zanedbatelné. Je
třeba si uvědomit, že vychýlení je z důvodu použití odhadu střední
hodnoty  místo skutečné střední hodnoty
místo skutečné střední hodnoty 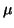 .
Pro
nevychýlený odhad rozptylu se používá vztah
.
Pro
nevychýlený odhad rozptylu se používá vztah
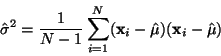 |
(19) |
Po odvození zjistíme, že střední hodnota tohoto odhadu je 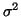 .
.
- 1
-
Athanasios Papoulis.
Probability and Statistics.
Prentice-Hall, 1990.
Tomas Svoboda
1999-03-17