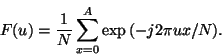2D Discrete Fourier Transform

Tomas Svoboda

Abstract:

This is assistant text for Signal and Image Processing subject. It reminds some properties of 2-D Discrete Fourier Transform and discrete convolution. It probably helps to solve problem of motion blur removing.

2D DFT

The discrete Fourier transform pair is

$\begin{displaymath}F(u,v) = \frac{1}{MN} \sum_{x=0}^{M-1}\sum_{y=0}^{N-1} f(x,y) \exp[-j2\pi(ux/M+vy/N)]. \end{displaymath}$

(1)

remind that

$\begin{displaymath}\exp[-j2\pi(ux/M+vy/N)] = \cos(2\pi(ux/M+vy/N)) - j \sin(2\pi(ux/M+vy/N)). \end{displaymath}$

(2)

Discrete Fourier transformation of discrete step function

Suppose discrete function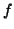

defined as

$\begin{displaymath} f[0,1,2,\dots,A] = 1, \ {\rm and} \ f[A+1,\dots,N-1] = 0. \end{displaymath}$

(3)

DFT is computed using

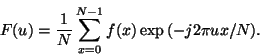$\begin{displaymath} F(u) = \frac{1}{N} \sum_{x=0}^{N-1} f(x) \exp{(-j2\pi ux/N)}. \end{displaymath}$

(4)

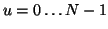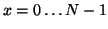Note discrete nature of $u = 0 \dots N-1$ and $x = 0 \dots N-1$ . Using (3) the equation (4) can be simplified to

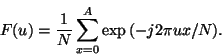$\begin{displaymath}F(u) = \frac{1}{N} \sum_{x=0}^{A} \exp{(-j2\pi ux/N)}. \end{displaymath}$

(5)

This summation gives the same value for each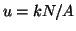

. The Fourier transform of the step function (3) is a periodic function with the period

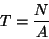$\begin{displaymath}T=\frac{N}{A} \end{displaymath}$

(6)

**Figure:** 1D discrete function.
$\includegraphics[width=0.9\textwidth]{fce1d.eps}$

**Figure 2:** Shifted amplitude of DFT of the function from the figure above.
$\includegraphics[width=0.9\textwidth]{fft1d.eps}$

1999-05-13