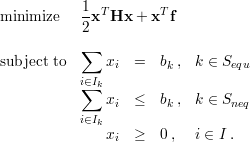
LIBQP is C library which implements algorithms for solving two special instances of convex Quadratic Programming (QP):
QP task with simplex constraints. This QP task is defined as follows
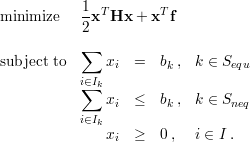
where  is the optimized vector,
is the optimized vector, 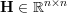 is a
symmetric positive semi-definite matrix,
is a
symmetric positive semi-definite matrix, 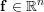 is a vector,
is a vector, 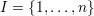 is
an index set,
is
an index set, 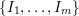 are subsets of
are subsets of 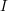 such that
such that 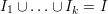 and
and 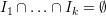 ,
, 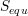 and
and  are index sets such that
are index sets such that
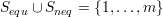 and
and 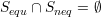 ,
, 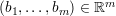 are
positive numbers.
are
positive numbers.
The implemented solver (libqp_splx.c) is a generalization of the method proposed in [1, 2]. It is based on the Sequential Minimal Optimization (SMO) algorithm with an improved working set selection strategy. Solving instances of this QP task is required, for example, in machine learning methods like Structured SVM learning, Bundle Methods for Risk Minimization, binary SVM with L2-soft margin, etc.
QP task with box constraints and a single linear equality constraint. This QP task is defined as follows
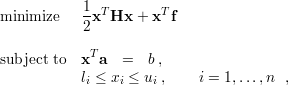
where  is the optimized vector,
is the optimized vector, 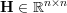 is a
symmetric positive semi-definite matrix,
is a
symmetric positive semi-definite matrix, 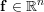 is a vector, a
is a vector, a 
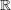 n is a vector
with non-zero entries, b
n is a vector
with non-zero entries, b 
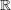 is a scalar, (l1,…,ln)
is a scalar, (l1,…,ln)  (
(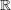 ∪{-∞})n and
(u1,…,un)
∪{-∞})n and
(u1,…,un)  (
(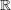 ∪{∞})n are lower and upper bounds, respectively.
∪{∞})n are lower and upper bounds, respectively.
The solver (libqp_gsmo.c) is the exact implementation of the Generalized Sequential Minimal Optimizer proposed in [3]. Solving this QP task is required, for example, when training binary SVM with L1-soft margin.
LIBQP is implemented in C language and interfaces to Matlab.
GNU/Linux. It should run also under Windows though not tested.
LIBQP can be downloaded from http://cmp.felk.cvut.cz/~xfrancv/libqp/libqp.zip.
cd libqp_root/matlab
|
libqp_compile
|
Now you can use libqp_splx and libqp_gsmo solvers located in libqp_root/matlab. To make these function visible from Matlab you need to add
addpath(’libqp_root/matlab’)
|
to your startup.m file.
To test the solvers run scripts
libqp_splx_test
libqp_gsmo_test |
cd libqp_root/examples
|
make
|
Now you can run test script
./run_test
|
LIBQP is licensed under the GPL version 3 ( http://gplv3.fsf.org/).
[1] V. Franc, V. Hlavac. A Novel Algorithm for Learning Support Vector Machines with Structured Output Spaces. Research Report K333 22/06, CTU-CMP-2006-04. May, 2006. ftp://cmp.felk.cvut.cz/pub/cmp/articles/franc/Franc-TR-2006-04.ps
[2] R.-E. Fan, P.-H. Chen, C.-J. Lin. Working Set Selection Using Second Order Information for Training SVM. JMLR. vol 6. 2005. TBA
[3] S.-S. Keerthi, E.G.Gilbert. Convergence of a Generalized SMO Algorithm for SVM Classifier Design. Technical Report CD-00-01, Control Division, Dept. of Mechanical and Production Engineering, National University of Singapore, 2000. http://citeseer.ist.psu.edu/keerthi00convergence.html