55:148 Digital Image Processing
55:247 Image Analysis and Understanding
Chapter 8, Part III
Image understanding: Point distribution
models
Point distribution models
- The Point Distribution Model (PDM) is a powerful shape description
technique that may subsequently be used in locating new instances of such
shapes in other images.
- It is most useful for describing features that have well understood
`general' shape, but which cannot be easily described by a rigid model.
- The PDM is a relatively recent development that has seen enormous
application in a short time.
- The PDM approach assumes the existence of a set of M examples (a training
set) from which to derive a statistical description of the shape and its
variation.
- In our context, we take this to mean some number of instances of the shape
represented by a boundary (a sequence of pixel co-ordinates).
- In addition, some number N of landmark points is selected on each
boundary; these points are chosen to correspond to a feature of the underlying
object.

- It is intuitively clear that if the hands so represented were in `about
the same place', so would the N landmark points be.
- Variations in the positions of these points would then be attributable to
natural variation between individuals.
- We may expect, though, that these differences would be `small' measured on
the scale of the overall shape.
- The PDM approach allows us to model these `small' differences (and,
indeed, to identify which are truly small, and which are more significant).
- Aligning the training data
- It is necessary first to align all the training shapes in an approximate
sense.
- This is done by selecting for each example a suitable translation, scaling
and rotation to ensure that they all correspond as closely as possible -
informally, the transformations are chosen to reduce (in a least squares
sense) the difference between an aligned shape and a `mean' shape derived from
the whole set.
- Specifically, suppose we wish to align just two shapes - each of these is
described by a vector of N co-ordinate pairs;
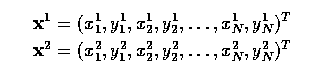
- A transform is composed of translation, rotation, and scaling represented
by matrix R applied to x2
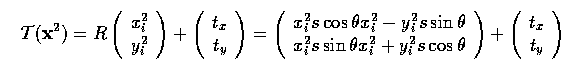
- The best transform can be found by minimizing
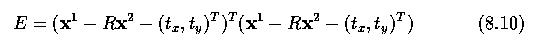
- This minimization is a routine application of a least squares approach -
partial derivatives of E are calculated with respect to the unknowns (theta,
s, tx and ty), and set to zero, leaving simultaneous
linear equations to solve.
- This general idea is used to co-align all M shapes using the following
algorithm;

- Step 3 of this algorithm is necessary since otherwise it is
ill-conditioned (underconstrained); without doing this, convergence would not
occur. Final convergence may be tested by examining the differences involved
in realigning the shapes to the mean.
- This approach assumes that each of the landmark points is of equal
significance, but that may not be the case. If for some reason one of them
moves around the shape less than others, it has a desirable stability that we
might wish to exploit during the alignment. This can be done by introducing a
(diagonal) weight matrix W into equation 8.10
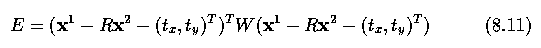
- The elements of W indicate the relative `stability' of each of the
landmarks in which a high number indicates high stability (so counts for more
in the error computation), and a low number the opposite.
- There are various ways of measuring this; one is to compute for each shape
the distance between landmarks k and l, and to let Vkl be the
variance in these distances.
- A high variance would indicate high mobility, and so setting the weight
for the k-th point to
-
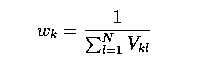
- would have the desired weighting effect.
- Knowledge of this mean allows explicit measurement of the variation and
co-variation exhibited by each landmark and landmark pair; we can write
- Doing this for each training vector, we can calculate the 2N x 2N
covariance matrix
- This matrix has some particularly useful properties.
- If we imagine the aligned training set plotted in 2N dimensions, it will
exhibit variation more in some directions than others (these directions will
not, of course, in general align with the co-ordinate axes) - these variations
are important properties of the shape we are describing.
- What these directions are, and their (relative) importance, may be derived
from an eigen-decomposition of S - that is, solving the equation

- Solutions to equation (8.12) provide the eigenvectors pi
and eigenvalues lambdai of S; conventionally, we assume
\lambdai >= \lambdai+1.
- It can be shown that the eigenvectors associated with larger eigenvalues
correspond to the directions of larger variation in the underlying data - they
provide the modes of variation.
- Thus solving the equation and finding the highest eigenvalues tells us
where the variation in the model is most likely to occur.
- It is well known that a set of eigenvectors provides a basis, meaning that
we can represent any vector x as a linear combination of the 2N different
pi. If we write
-
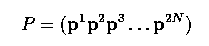
- then for any vector x, a vector b exists such that
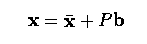
- where the components of b indicate how much variation is exhibited with
respect to each of the eigenvectors.
- Using the observation that the eigenvectors of lower index describe most
of the changes in the training set, we may expect that the contributions from
p2N, p2N+1, ... will play a small role, thus


- will be good for sufficiently high t
- This permits a dimensional compression of the representation - if there is
a lot of structure in the data, t will be low (relative to 2N) and good shape
description will be possible very compactly by representing the shape as
bt rather than x.
- One approach to this is to calculate lambdatotal, the sum of
the lambdai, and choose t such that
- The choice of alpha here will govern how much of the variation seen in the
training set can be recaptured by the compacted model.
- Further, it can be shown that the variance of bi over the
training set will be the associated lambdai; accordingly, for `well
behaved' shapes we might expect
-
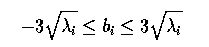
- - that is, most of the population is within 3 sigma of the mean.
- This allows us to generate, from knowledge of P and lambdai,
plausible shapes that are not part of the training set.
Example - Metacarpal analysis
- We can illustrate this theory with an example taken from automatic hand
X-ray analysis.
- The finger bones (metacarpals) have characteristic long, thin shape with
bulges near the ends - precise shape differs from individual to individual,
and as an individual ages.
- Scrutiny of bone shape is of great value in diagnosing bone aging
disorders and is widely used by pediatricians.
- From a collection of X-rays, 40 landmarks (so vectors are 80 dimensional)
were picked out by hand on a number (approximately 50) of segmented
metacarpals.
- Next figure illustrates (after alignment) the mean shape, together with
the actual positions of the landmark points from the entire data set.

- The covariance matrix and its eigenvectors associated with the
variation are extracted; the relative contribution of the most influential
components is illustrated in Table~\ref{tab.PDM}.
- From this we see that more than 95% of the shape variation is captured by
the first eight modes of variation.
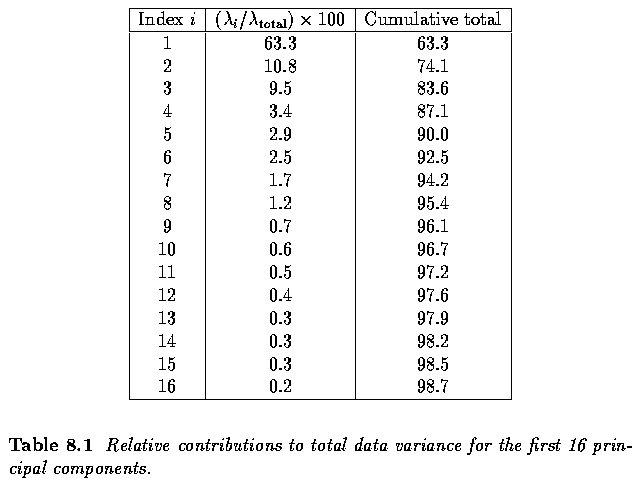
- Next figure illustrates the effect of varying the first mode of the mean
shape by up to 2.5 sqrt{lambda_1}.
- This mode, which accounts for more than 60% of the variation seen in the
data, captures the (asymmetric) thickening and thining of bones (relative to
their length) which is an obvious characteristic of maturity.
- In this example, it is clear that 2.5 is an unlikely factor for
sqrt{lambda_1} since the resulting shapes are too extreme - thus we may expect
b_1 to be smaller in magnitude for this application.
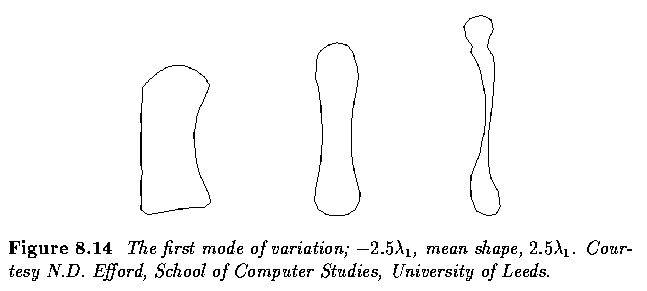
- Next figure similarly illustrates extremes of the third mode.
- The shape change here is somewhat subtler; part of what is captured is a
bending (in banana fashion) of the bone.
- Both extremes have a plausible `bone-like' look about them.
Fitting models to data
- A strength of this approach is that it permits plausible shapes to be
fitted to new data.
- Given an image in which we wish to locate an instance of a modelled shape
(specifically, given an edge map of the image, so having information about
where boundaries are most likely to lie), we require to know
- the mean shape x
- the transformation matrix P_t
- the particular shape parameter vector b_t
- the particular pose (translation, rotation, scale)
- The mean shape and the transformation matrix are known from the model
construction
- The identification of b_t and the pose is an optimization problem
- locate the parameters that best fit the data at hand, subject to certain
constraints.
- These constraints would include the known limits on reasonable values
for the components of b_t, and might also include domain knowledge about
plausible positions for the object to constrain the pose.
- In the metacarpal example, this would include knowledge that a bone lies
within the hand silhouette, is aligned with the finger and is of a known
approximate size.
- This approach may be used successfully with a number of well known
optimization algorithms.
- It is likely, however, that convergence would be slow.
- An alternative, quicker approach is to use the PDM as the basis of an
Active Shape Model (ASM).
- Here, we iterate toward the best fit by examining an approximate fit,
locating improved positions for the landmark points, then recalculating pose
and parameters.
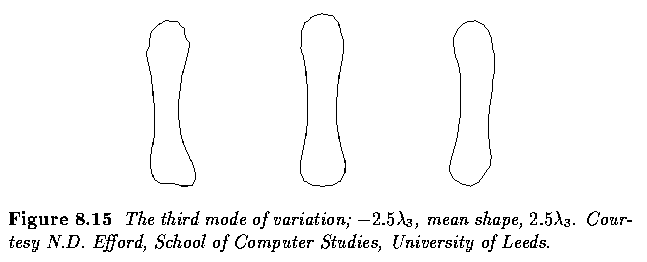
Fitting an active shape model (ASM)



- Step 2 assumes that a suitable target can be found, which may not always
be true.
- If there is none, the landmark can be left where it is, and the model
constraints will eventually pull it into a reasonable position.
- There is also the option of locating targets by more sophisticated means
than simple intensity gradient measurements.
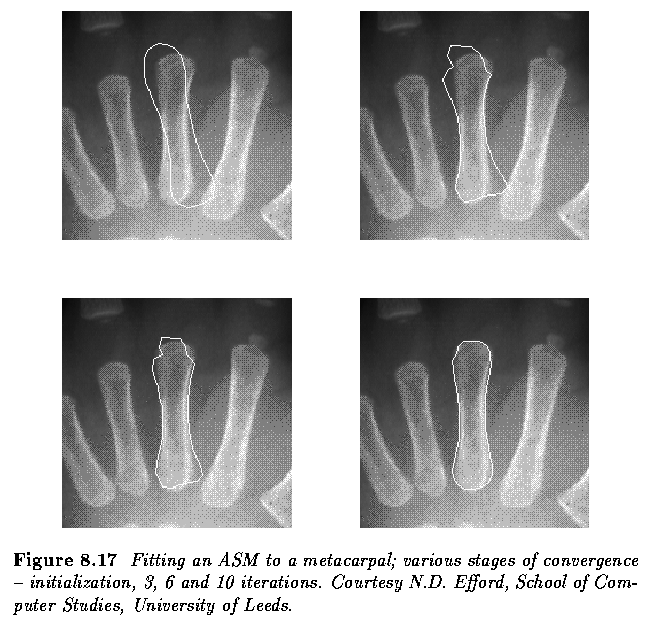
- The algorithm is illustrated in the next figure.
- Note that the model locates the correct position despite the proximity of
strong boundaries that could distract it - this does not occur because the
shape of the boundary is tightly bound in.
Extensions
- In a short time, the literature on PDMs and ASMs has become very extensive
- the technique lends itself to a very wide range of problems, but has some
drawbacks.
- The placing of the landmark points for construction of the training
set is clearly very labor intensive, and in some application error-prone.
- Automatic placing of these points has been addressed.
- Efficiency of the approach has also been enhanced by the common idea of a
multi-resolution attack.
- Using a coarse-to-fine strategy can produce benefits in both quality of
final fit, and reduction of computational load
- As presented, the approach is strictly linear in the sense that control
points may only move along a straight line (albeit with respect to directions
of maximum variation);
- non-linear effects are produced by combining contributions from
different modes;
- aside from being imperfect, this results in a representation that is not
as compact as it might be if the non-linear aspects were explicitly modeled.
- This problem has been addressed in two ways;
- introduction of the Polynomial Regression PDM which assumes dependence
between the modes, with minor modes being polynomial combinations of major
ones, and
- extension of the linear model by permitting polar relationships between
modes, thereby efficiently capturing the ability of (parts of) objects to
rotate around one another.
Last Modified: April 1, 1997
![[Go Back]](lecture_pdf_sonka/next.gif)


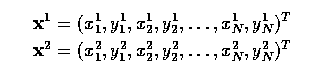
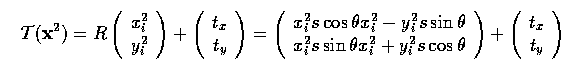
![]()

![]()
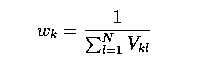
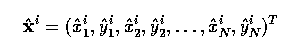
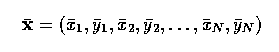
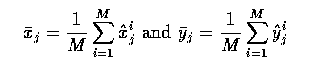
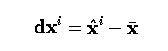
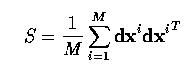

![]()

![]()

![]()








