Transformations

Transformations in the images are represented by homographies of ${\cal P}^2 \rightarrow {\cal P}^2$. A homography of ${\cal P}^2 \rightarrow {\cal P}^2$ is represented by a $3 \times 3$-matrix ${\bf H}$. Again ${\bf H}$ and $\lambda {\bf H}$ represent the same homography for all nonzero scalars $\lambda$. A point is transformed as follows:

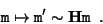$${\tt m} \mapsto {\tt m}' \sim {\bf H} {\tt m} \enspace .$$ (B5)

The corresponding transformation of a line can be obtained by transforming the points which are on the line and then finding the line defined by these points:

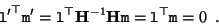$${\tt l'}^\top {\tt m'} = {\tt l}^\top {\bf H}^{-1} {\bf H} {\tt m} = {\tt l}^\top {\tt m} = 0 \enspace .$$ (B6)

From the previous equation the transformation equation for a line is easily obtained (with ${\bf H}^{-\top} = ({\bf H}^{-1})^\top = ({\bf H}^\top)^{-1}$):

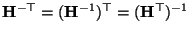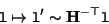$${\tt l} \mapsto {\tt l'} \sim {\bf H}^{-\top} {\tt l}$$ (B7)

Similar reasoning in ${\cal P}^3$ gives the following equations for transformations of points and planes in 3D space:

$${\tt M} \mapsto {\tt M}' \sim {\bf T} {\tt M}\, ,$$ (B8)

$${\tt\Pi} \mapsto {\tt\Pi}' \sim {\bf T}^{-\top} {\tt\Pi}\,$$ (B9)

where ${\bf T}$ is a $4 \times 4$-matrix.