2D mapping

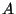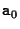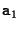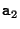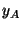The following approaches will use this formalism to map images onto planes and vice versa. We define a local coordinate system in a plane $A$ giving one point ${\tt a}_0$ on the plane and two vectors ${\tt a}_1$ and ${\tt a}_2$ spanning the plane. So each point $p$ of the plane can be described by the coordinates $x_A$, $y_A$: $p = [ {\tt a}_1\, {\tt a}_2\, {\tt a}_0][x_A\,y_A\,1]^\top$. 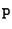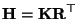The point ${\tt p}$ is perspectively projected into a camera which is represented by the $3 \times 3$ matrix ${\bf H = KR}^\top$ and the projection center ${\tt c}$. The matrix 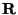${\bf R}$ is the orthonormal rotation matrix and ${\bf K}$ is an upper triangular calibration matrix. The resulting image coordinates $x,y$ are determined by $[x\,y \,1]^\top \sim {\bf H}{\tt p} -{\bf H}{\tt c}$. 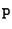Inserting the above equation for ${\tt p}$ results in

$$\left[ \begin{array}{c} x \\ y\\ 1 \end{array} \right] \sim ... ...] \left[ \begin{array}{c} x_A \\ y_A\\ 1 \end{array} \right]$$ (H1)

Each mapping between a local plane coordinate system and a camera can be described by a single $3 \times 3$ matrix ${\tt B} = {\tt H} [{\tt a}_1 \, {\tt a}_2 \, ({\tt a}_0-{\tt c}) ]$.