Mapping via local planes

The results can be further improved by considering local depth maps. Spending more time for each view, we can calculate the approximating plane of geometry for each triangle in dependence on the actual view. This improves the accuracy further as the approximation is not done for the whole scene but just for that part of the image which is seen through the actual triangle. The depth values are given as functions 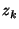$z_k$ of the coordinates in the recorded images $z_k ([x_k \, y_k\, 1]^\top)$. They describe the distance of a point perpendicular to the image plane. Using this depth function, we calculate the 3D coordinates of those scene points which have the same 2D image coordinates in the virtual view as the projected camera centers of the real views. 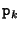The 3D point ${\tt p}_k$ which corresponds to the real camera 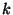$k$ can be calculated as 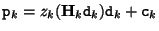${\tt p}_k = z_k ({\bf H}_k{\tt d}_k){\tt d}_k + {\tt c}_k$, where 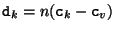${\tt d}_k=n({\tt c}_k - {\tt c}_v)$. The function $n$ scales the given 3D vector such, that its third component equals one. 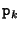We can interpret the points ${\tt p}_k$ as the intersection of the line $\overline{{\tt c}_V{\tt c}_k}$ with the scene geometry. Knowing the 3D coordinates of triangle corners, we can define a plane through them and apply the same rendering technique as described above.