Master Thesis : Reconstructing 3D mesh from video sequence

Thesis

Abstract       This thesis aims to create complete 3D reconstruction of real scene from uncalibrated video sequence. My work deals with image features correspondence problem reduced to feature tracking throughout image sequence, camera tracking with retrieving cameras positions and camera calibration, and finally dense scene reconstruction represented in 3D mesh.       Even input consists of un-calibrated images, algorithm assumes that images were taken by camera with these restrictions to intrinsic parameters: zero-skew, principal point is at image center and aspect ratio of 1. Camera focal length can vary across the sequence. Images must be processed in the order of how they were captured. Motion between two consequent frames is assumed to be small.       Main contribution of this work is in simple feature detector and tracker, novel fast on-line structure from motion algorithm based on two-view geometry, dense reconstruction based on new stereo algorithm and 3D mesh extraction. In this work I also describe linear method for calibrating cameras only from input image (self-calibration). Experimental method for lens radial distortion detection based on two-view geometry is also presented here. 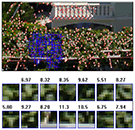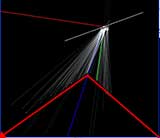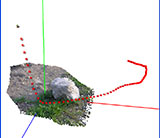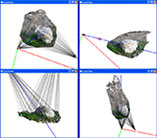Achieved results Tracking process Good feature to track Skipped feature Detector Guided matching Structure from motion Quasi calibrated pair From top view Sequence Dense reconstruction Rectification Disparity (blue) Result Video Following video were compressed using DivX 5 codec. Pipeline Human Girl in a train Medusa original sequence by [1] Rock Object Additional video Cescg 2005 - structure from motion overview Cescg 2005 - dense reconstruction Conclusion and future work       This thesis presented a sequential approach for creating calibrated motion and structure from un-calibrated video sequence with dense 3D reconstruction of the space. Sequential processing allows us to process input video directly from camera stream. Biggest advantage of processing from stream is that we can skip process of storing to disk and v?ideo compression which leads to better quality (due to uncompressed transfer).       Because there is always a noise in the images it is not good to calculate camera position from only two views. Therefore in future it would be better to improve camera projection matrix calculation, using more images, maybe using factorization approach. My experiences with real camera also showed that if principal point is not in image centre, than scene stay skewed even after self-calibration. For cheap hand held cameras it is unexpected to have principal point at image center. Allowing principal point to be constant (non zero) or to be varying leads to non-linear self-calibration algorithm [4].       Since there are always many ambiguities in dense reconstruction process I recommend using algorithm where user can control algorithm pipeline. This is possible and effective when algorithm responds to user interaction promptly. Slowest part in my reconstruction pipeline is algorithm for dense reconstruction. Because it works in rectified space, more scan lines can be processed parallel and thus it is possible to drop down response time.       More work need to be done also in process of triangulation. It would be better to extract dense point cloud and generate surface using point cloud approximation algorithms. Bibliography: M. Pollefeys - L. Van Gool - M. Vergauwen - F. Verbiest - K. Cornelis - J. Tops - R. Koch. Visual modeling with a hand-held camera, International Journal of Computer Vision 59(3), 207-232, 2004. M. Han - T. Kanade. Creating 3D Models with Uncalibrated Cameras, proceeding of IEEE Computer Society Workshop on the Application of Computer Vision (WACV2000), December 2000. P. Sturm - B. Triggs. A Factorization Based Algorithm for Multi-Image Projective Structure and Motion, 4th European Conference on Computer Vision, Cambridge, England, April 1996, pp. 709-720 . R. Hartley - A. Zisserman. Multiple View Geometry In Computer Vision. Second Edition. Cambridge University press, UK. March 2004. A. W. Fitzgibbon -- A. Zisserman. Automatic Camera Tracking. Robotics Research Group. Department of Engineering Science. University of Oxford, UK. S. Birchfileld. KLT: An Implementation of the Kanade-Lucas-Tomasi Feature Tracker. Stanford University, http://vision.stanford.edu/~birch C. Harris - M. Stephens. A combined corner and edge detector, Fourth Alvey Vision Conference pp.147-151, 1988. M. Fischler -- R. Bolles. Random Sample Consensus: A Paradigm for Model Fitting. Communications of the ACM, 24 (6), 381-395. 1981. R. Hartley, In defense of the eight-point algorithm. IEEE Trans. On Pattern Analysis and Machine Intelligence, 19(6):580-593, June 1997. A. W. Fitzgibbon. Simultaneous linear estimation of multiple view geometry and lens distortion. Department of Engineering Science. University of Oxford, UK. W. Press -- S. Teukolsky -- W. Vetterling. Numerical recipes in C : the art of scientific computing, Cambridge university press, 1992 B. Triggs -- P. McLauchlan -- R. Hartley -- A. Fitzgibbon. Bundle Adjustment - Modern Synthesis, Vision Algorithms: Theory and Practice, Springer Verlag, 298-375, 2000. M. I. A. Lourakis - A. A. Argyros. The Design and Implementation of a Generic Sparse Bundle Adjustment Software Package Based on the Levenberg-Marquardt Algorithm, Institute of Computer Science -- FORTH, Heraklion, Crete, Greece, August 2004. B. Triggs. The absolute Quadric, Proc. 1997 Conference on Computer Vision and Pattern Recognition, IEEE Computer Society press, pp. 609-617, 1997. M. Pollefeys -- R. Koch -- L. V. Gool. Self-Calibration and Metric Reconstruction in spite of Varying and Unknown Intrinsic Camera Parameters, International Journal of Computer Vision, KLuwer Academic Publishers, Boston, 1998 P. Breadsley -- A. Zisserman -- D. Murray. Sequential Updating of Projective and Affine Structure from Motion. International Journal of Computer Vision (23), No. 3, Jun-Jul 1997, pp. 235-259. M. Pollefeys. 3D Photography, comp290-89 Fall, University of North Carolina, 2004. V. Kvasnička -- J. Pospíchal -- P.Tiňo. Evolučné algoritmy. Slovak technical university, Bratislava, 2000 K. N. Kutulakos - S. M. Seitz, A Theory of Shape by Space Carving, Proc. Seventh Int'l Conf. Computer Vision, vol. 1, pp. 307-314, 1999. V. Kolmogorov - R. Zabih. Multi-Camera Scene Reconstruction via Graph Cuts, Proc. Seventh European Conf. Computer Vision, 2002. G. Zeng - S. Paris - L. Quan - M. Lhuillier. Surface Reconstruction by Propagating 3D Stereo Data in Multiple 2D Images, Dep. of Computer Science, HKUST, Clear Water Bay, Kowloon, Hong Kong M. Lhuillier - L. Quan. A Quasi-Dense Approach to Surface Reconstruction from Uncalibrated Images, IEEE Trans. On Pattern Analysis and Machine Intelligence, VOL. 27, NO. 3, MARCH 2005 I. Cox - S. Hingorani - S. Rao. A Maximum Likelihood Stereo Algorithm, Computer Vision and Image Understanding, Vol. 63, No. 3., 1996 S. Birchfield - C. Tomasi, Depth Discontinuities by Pixel-to-Pixel Stereo, International Journal of Computer Vision, 35(3): 269-293, December 1999 S. M. Seitz - C. R. Dyer. Photorealistic Scene Reconstruction by Voxel Coloring. International Journal of Computer Vision, 35(2), 151-173. 1999 Culbertson - W. B., T. Malzbender - G. Slabaugh: 1999, `Generalized Voxel Coloring. In: Workshop on Vision Algorithms: Theory and Practice. Corfu, Greece. M. Okutomi - T. Kanade. A multiple baseline stereo. IEEE Trans. On Pattern Analysis and Machine Intelligence, 15, 1993. C. Strecha, R. Fransens, L. Van Gool - Wide-baseline Stereo from Multiple Views : a Probabilistic Account, ESAT-PSI, University of Leuven, Belgium C. R. Dyer. Volumetric scene reconstruction from multiple views, FIU01, 2001, 469-489

© 2005 Martin Bujnak. All rights reserved.