In quantum physics, so-called entangled quantum states play an important role. Quantum entanglement occurs when a group of particles interact in such a way that the quantum state of each particle of the group cannot be described independently of the state of the others. A famous one is the Greenberger–Horne–Zeilinger state.

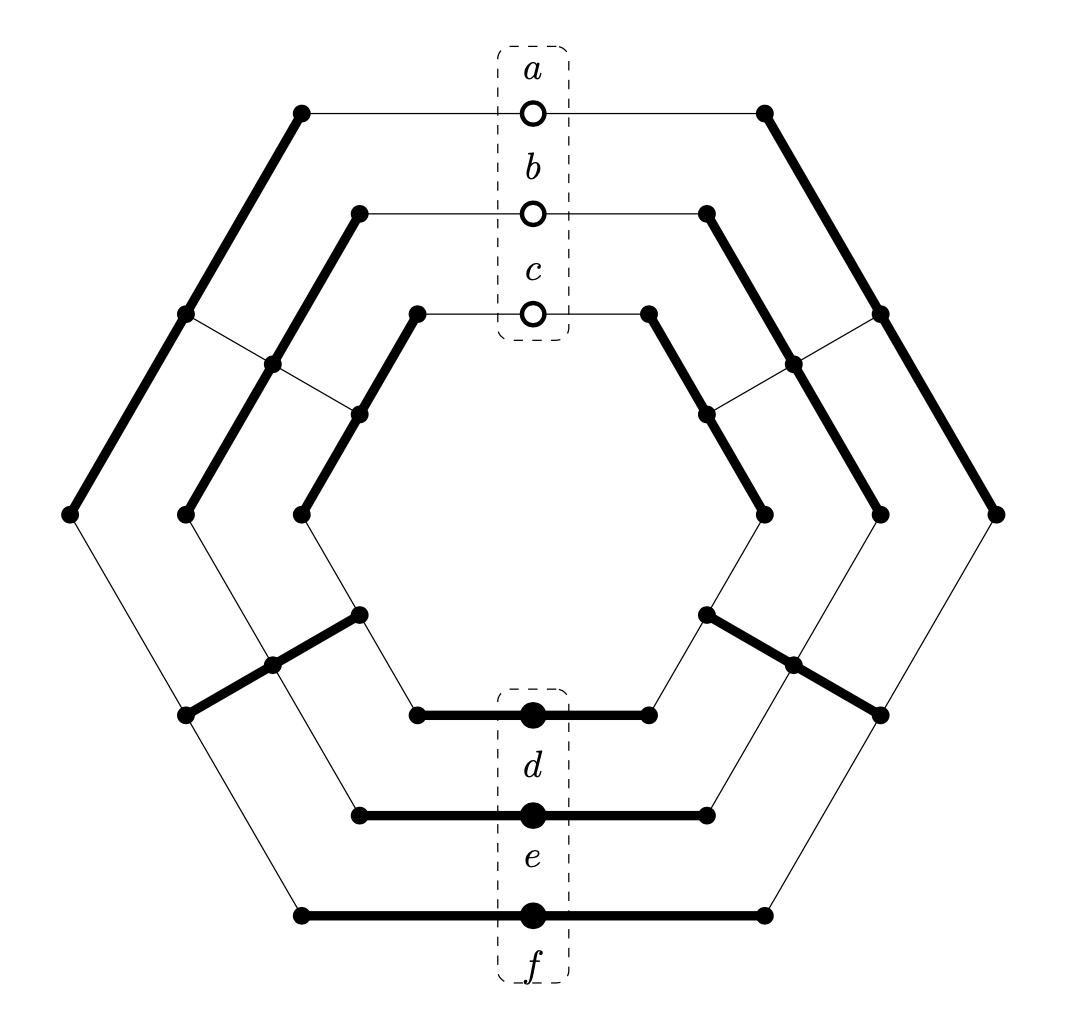
We studied a diagram related to entanglement, which has specific properties.*

To prove that such a configuration is realistic, we had to show that it is the orthogonality diagram of a real set of vectors in 3D. We accomplished this in a joint work with Karl Svozil from TU Wien.

We used only elements of 3D geometry, thus the topic can be understood also by a wider audience not necessarily familiar with quantum logics.

Daniel Greenberger (middle), Anton Zailinger (right); our diagram (background)

*For insiders: The diagram represents a quantum logic (orthomodular lattice) with elements a, b, c, d, e, f such that, for any probability measure P, we have P(a)+P(b)+P(c) = P(d)+P(e)+P(f), while this sum can be almost arbitrary.