Snow calamity
The northern region of a small country includes several towns. The road network between the towns consists of main
and secondary roads. Each main road connects a pair of towns. The main roads do not cross each other outside towns.
For a pair of towns, there is at most one road that connects them directly.
It is always possible to travel from one town to another using only the main roads.
For administrative purposes, each town T has its own unique numeric identifier id(T).
Let rd(T1, T2) denote the minimum number of main roads that have to be used to reach town
T2 from town T1 (as well as town T1 from town T2) without the use
of secondary roads.
Some of the towns are district towns. Every town in the region belongs to exactly one district. For each town T, its district town D
meets the following:
For any district town D′ other than D
- rd(T, D) ≤ rd(T, D′), and
- rd(T, D) = rd(T, D′) implies id(D) < id(D′).
In winter, a calamity occurs in the whole region. Overnight, all roads are covered with a massive layer of snow.
Some of the main roads need to be cleared of snow as soon as possible to re-establish mutual connections for all towns in the region, which means that, for
each pair of towns, there must be some main roads cleared of snow that allow to travel between the towns.
The process of snow removal is supposed to have two phases. First, each district will ensure the renewal of connections for each pair of its
towns. After that, all the districts will cooperate
and ensure the renewal of connections for each pair of towns in the whole region.
The cost for clearing any particular main road of snow is known. This cost remains the same for the first and second phase.
The question is, what snow removal plan should be chosen to minimize the overall cost.
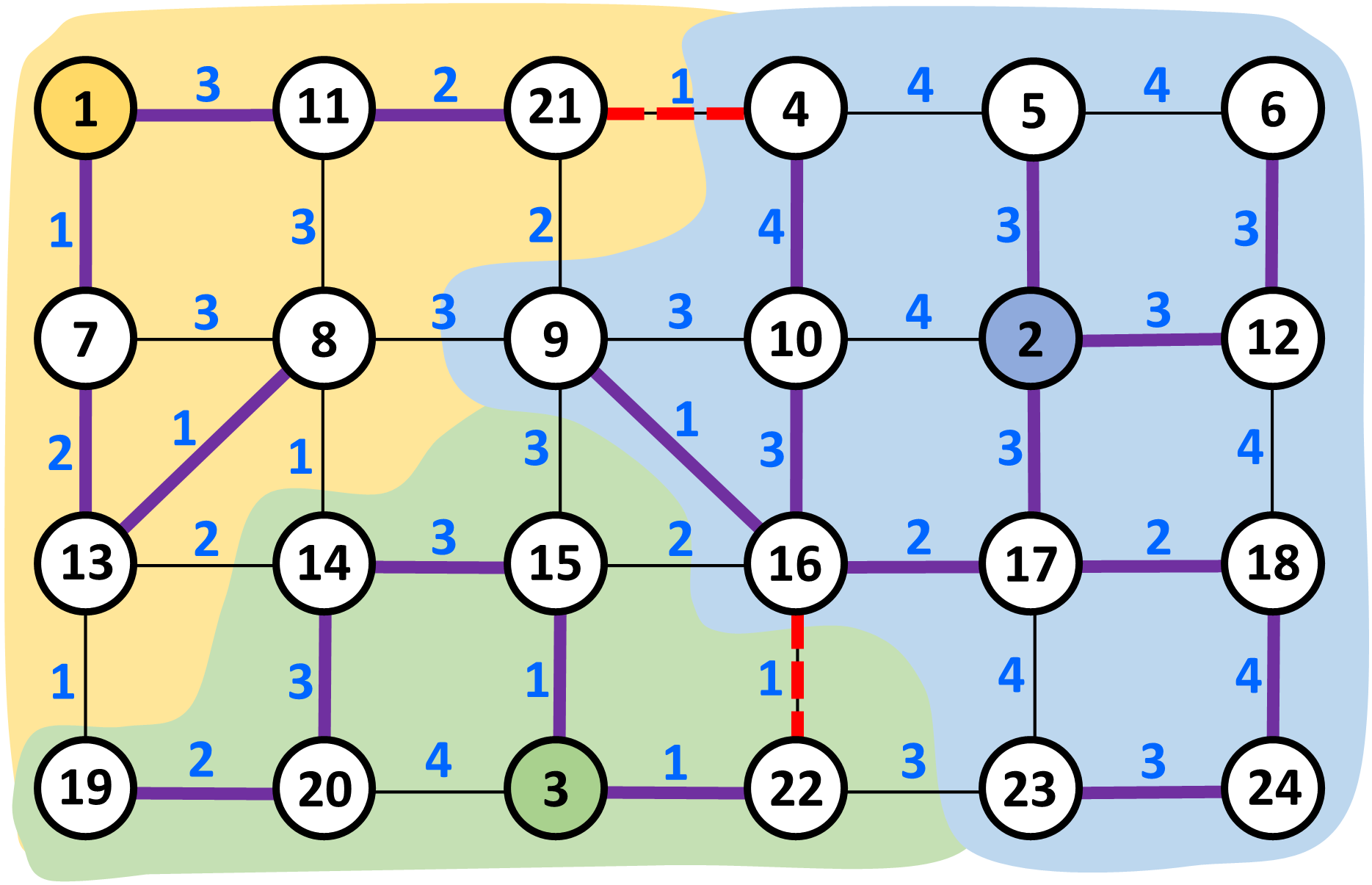
Figure 1. The scheme depicts all towns (nodes) and main roads (edges) in the region.
District towns have identifiers 1, 2 and 3. The colored backgrounds show towns in their districts. Blue numbers along the edges are costs
for snow removal on a given road.
An optimal solution is indicated by purple and dashed red edges. Purple roads are made operational during the first phase. They connect
towns within districts. Dashed red roads are made operational during the second phase. They ensure the connection for any pair of
towns throughout the region. The total cost of implementing this plan is 52.
|
The task
The topology of the main roads between the towns in the region and the costs for clearing them of snow are given.
It is also known which towns are district towns. Find an optimal snow removal plan that follows the defined
two-phase strategy and minimizes the sum of costs paid for clearing selected main roads.
Input
The first input line contains three integers T, D, R, separated by spaces. T is the number of towns, D
is the number of district towns, R is the number of main roads. Towns are numbered from 1 to T, district towns are numbered from
1 to D. These numbers correspond to town id's.
R input lines representing the main roads follow. Each of them contains three integers T1,
T2, C, separated by spaces, that represent the main road between towns T1 and T2.
Integer C is the cost for clearing this road of snow. The roads are listed in random order.
It holds T ≤ 2.5 × 105, D ≤ 2000, R ≤ 4.5 × 105. The cost for clearing
any main road of snow is positive and not greater than 250.
Output
The output contains one line with one integer which equals the minimum total cost for clearing main roads of snow in both phases.
Example 1
Input
6 2 7
2 4 3
3 1 5
2 1 4
5 3 5
6 4 3
3 4 4
6 5 2
Output
18
| |
Example 2
Input
24 3 40
12 2 3
7 13 2
7 8 3
14 20 3
3 22 1
21 4 1
23 24 3
12 18 4
10 2 4
9 10 3
18 24 4
16 10 3
15 9 3
16 9 1
14 8 1
2 5 3
9 8 3
15 14 3
3 15 1
13 14 2
4 5 4
13 19 1
| |
8 11 3
8 13 1
16 17 2
6 12 3
6 5 4
23 17 4
17 18 2
1 7 1
10 4 4
20 3 4
21 11 2
16 15 2
19 20 2
17 2 3
22 23 3
1 11 3
22 16 1
21 9 2
Output
52
The data of Example 2 is depicted in Figure 1.
Public data
The public data set is intended for easier debugging and approximate program correctness checking. The public data set is stored also in the upload system and each time a student submits a solution it is run on the public dataset and the program output to stdout and stderr is available to him/her.
Link to public data set
