Příklady na pravděpodobnost - Řešení
Podmíněná pravděpodobnost jevu 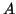 z předpokladu, že nastane jev
z předpokladu, že nastane jev 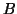
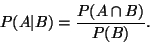 |
(1) |
Dokažte, že podmíněná pravděpodobnost splňuje tři základní axiomy
pravděpodobnosti.
- 1.
-
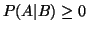 .
To je zřejmé ihned z definice.
.
To je zřejmé ihned z definice.
- 2.
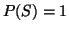 .
.
- 3.
- Jestliže
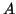 a
a 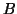 jsou vzájemně se vylučující jevy.
jsou vzájemně se vylučující jevy.
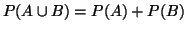 .
.
Důkaz: Jelikož 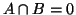 ,
pak také
,
pak také
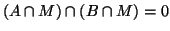 .
A jelikož
.
A jelikož
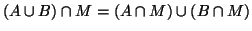 pak tedy
pak tedy
Předpokládejme, že
![$[A_1,\dots,A_n]$](img13.gif) jsou vzájemně se vylučující jevy
z jevového pole
jsou vzájemně se vylučující jevy
z jevového pole 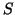 .
Pravděpodobnost
.
Pravděpodobnost 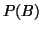 jevu
jevu 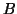 je
je
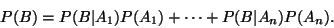 |
(2) |
Dokažte platnost vztahu pro úplnou pravděpodobnost.
Jelikož
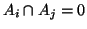 pro
pro 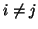 pak také samozřejmě
pak také samozřejmě
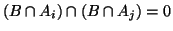 .
Čili s použitím třetího axiomu
pravděpodobnosti platí
.
Čili s použitím třetího axiomu
pravděpodobnosti platí
Rovnice (2) plyne z faktu
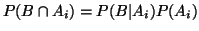 .
.
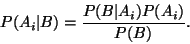 |
(3) |
Dokažte Bayesův vzorec.
Z rovnice (1) plyne
tudíž
Odtud platnost rovnice (3).
Jevy 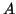 a
a 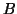 jsou statisticky nezávislé, jestliže platí:
jsou statisticky nezávislé, jestliže platí:
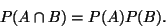 |
(4) |
V krabici je 5 koulí. 3 jsou bílé a 2 černé. Vytáhnu dvě koule za
sebou. Jaká je pravděpodobnost, že první vytáhnu bílou a druhou
černou?
Pravděpodobnost, že první vytahnu bílou je
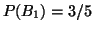 .
Po vytažení
první zbydou 2 a 2 koule různé barvy. Čili podmíněná pravděpodobnost
.
Po vytažení
první zbydou 2 a 2 koule různé barvy. Čili podmíněná pravděpodobnost
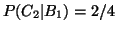 .
Z rovnice (1) odvodíme
.
Z rovnice (1) odvodíme
Student jde na zkoušku, ale neví, který ze tří možných předmětů
(RPZ,PV,PG) se zkouší. Ví, že neumí 40% otázek z RPZ, 15% z PV a 20% z PG.
- 1.
- Jaká je pravděpodobnost, že bude vyhozen?
- 2.
- Jaká je pravděpodobnost, že bude vyhozen z RPZ?
- 3.
- Bude-li vyhozen, jaká je pravděpodnost toho, že to bude z RPZ?
Pravděpodnosti zkoušky z jednotlivých předmětů jsou si rovny.
Podmíněné pravděpodobnosti vyhození jsou
- 1.
- Z rovnice (2) vyplývá
pravděpodobnost vyhození
- 2.
- Pravděpodobnost, že bude vyhozen z RPZ.
- 3.
- Z Bayesova vzorce (3) plyne
Dva milenci 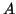 a
a 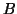 se domluví, že každý přijde mezi 17. a 18.
hodinou na smluvené místo. Každý počká 15 minut, nedočká-li se
druhého, odejde.
se domluví, že každý přijde mezi 17. a 18.
hodinou na smluvené místo. Každý počká 15 minut, nedočká-li se
druhého, odejde.
- 1.
- Jaká je pravděpodobnost, že milenec
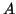 přijde před
přijde před 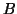 .
.
- 2.
- Jaká je pravděpodobnost, že se na smluveném místě
setkají?
- 3.
- Předpokládejme, že se sejdou. Jaká je pravděpodobnost, že
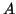 přijde před
přijde před 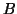 .
.
Oprostíme se od hodinových údajů a specifikujeme, jako dobu příchodu
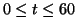 minut. Nejprve specifikujme model. Výstup jednoho
experimentu (schůzky) je dvojice příchodů
minut. Nejprve specifikujme model. Výstup jednoho
experimentu (schůzky) je dvojice příchodů 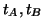 .
Jevový prostor je
tedy čtverec o hraně 60 minut. Definujeme jev
.
Jevový prostor je
tedy čtverec o hraně 60 minut. Definujeme jev 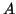 jako příchod milence
jako příchod milence
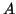 v časovém rozmezí
v časovém rozmezí
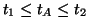 .
.
obdobně
Za předpokladu nezávislosti příchodů platí
Tudíž pravděpodobnost libovolného jevu 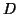 může být vyjádřena jako
může být vyjádřena jako
- 1.
- Jev
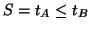 Plocha příznivá jevu
Plocha příznivá jevu 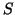 je trojúhelník
je trojúhelník 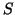 ,
viz obrázek 1. Tudíž
,
viz obrázek 1. Tudíž
- 2.
- Jev
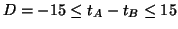 .
Plocha mnohoúhelníku
.
Plocha mnohoúhelníku 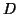 na obrázku 1 odpovídá jevu
na obrázku 1 odpovídá jevu 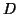 .
Tudíž
.
Tudíž
- 3.
-
Figure 1:
Specifikace modelu.
![\includegraphics[width=0.6\textwidth]{Figs/milenci.eps}](img48.gif) |
Tomas Svoboda
1999-03-09