The projective plane

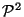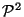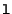The projective plane is the projective space ${\cal P}^2$. A point of ${\cal P}^2$ is represented by a 3-vector ${\tt m}=[x \, y\, w]^\top$. A line ${\tt l}$ is also represented by a 3-vector. A point 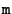${\tt m}$ is located on a line 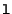${\tt l}$ if and only if

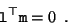$${\tt l}^\top {\tt m} = 0 \enspace .$$ (B1)

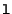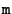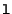This equation can however also be interpreted as expressing that the line ${\tt l}$ passes through the point ${\tt m}$. This symmetry in the equation shows that there is no formal difference between points and lines in the projective plane. This is known as the principle of duality. A line ${\tt l}$ passing through two points ${\tt m_1}$ and ${\tt m_2}$ is given by their vector product 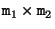${\tt m}_1 \times {\tt m}_2$. This can also be written as

$${\tt l} \sim [{\tt m}_1]_\times {\tt m}_2 \mbox{ with } [{\t... ...w_1 & 0 & x_1\\ y_1 & -x_1 & 0 \end{array}\right] \enspace .$$ (B2)

The dual formulation gives the intersection of two lines. All the lines passing through a specific point form a pencil of lines. If two lines 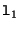${\tt l}_1$ and ${\tt l}_2$ are distinct elements of the pencil, all the other lines can be obtained through the following equation:

$${\tt l} \sim \lambda_1 {\tt l}_1 + \lambda_2 {\tt l}_2$$ (B3)

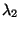for some scalars $\lambda_1$ and $\lambda_2$. Note that only the ratio $\frac{\lambda_1}{\lambda_2}$ is important.