



Next: Transformation of a quadric/dual
Up: Conics and quadrics
Previous: Tangent to a quadric
Contents
When  varies along the quadric, it satisfies
varies along the quadric, it satisfies
 and thus the tangent plane
and thus the tangent plane 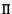 to
to  at
at  satisfies
satisfies
 . This shows that the tangent planes to a quadric
. This shows that the tangent planes to a quadric  are belonging to a dual quadric
are belonging to a dual quadric
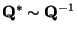 (assuming
(assuming  is of full rank).
is of full rank).
Marc Pollefeys
2000-07-12