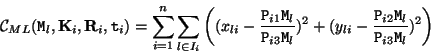 |
(F24) |
The calibration results could be refined even more through a Maximum Likelihood approach. Traditionally several assumptions are made in this case. It is assumed that the error is only due to mislocalization of the image features. Additionally, this error should be uniformly and normally distributedF5. This means that the proposed camera model is supposed to be perfectly satisfied. In these circumstances the maximum likelihood estimation corresponds to the solution of a least-squares problem. In this case a criterion of the type of equation (6.2) should be minimized:
An interesting extension of this approach would be to introduce some uncertainty on the applied camera model and self-calibration constraints. Instead of having hard constraints on the intrinsic camera parameters imposed through the parameterization, one could impose soft constraints on these parameters through a trade-off during the minimization process. This would yield a criterion of the following form:
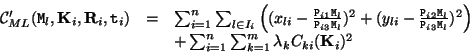 |
(F25) |