Shluková analýza K-Means

Cílem tohoto cvičení je implementovat algoritmus K-means a následně ho použít pro dvě rozdílné úlohy: pro odhad parametrů gaussovské směsi a pro úlohu "učení bez učitele". Cvičení je jednoduché, ale poměrně obsáhlé. Doporučujeme si proto alespoň některé body připravit již v rámci domácí přípravy.

Zadání:

Část 1: Implementace K-means

Prostudujte si materiály ke cvičení [1] a implementujte algoritmus K-means.

Úkoly:
  1. Nahrajte si cvičná data data.mat, zobrazte si je pomocí funkce ppatterns().
    - soubor data.mat obsahuje proměnnou X - 2xN pole 2D bodů.
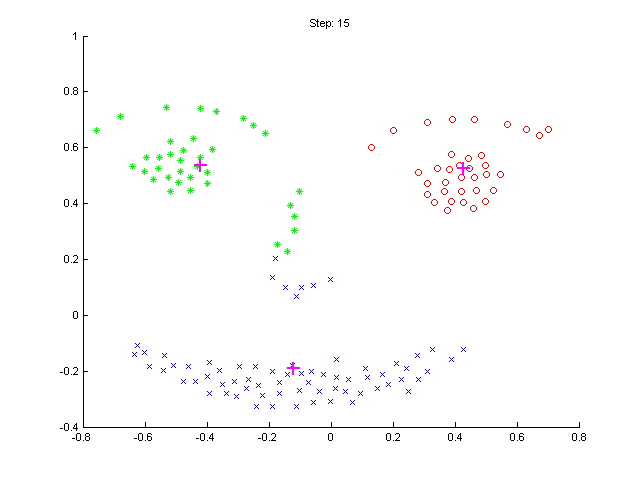
  2. V každé iteraci algoritmu vykreslujte polohu průměrů μj a klasifikaci dat (tj. příslušnost k danému μj). K vykreslování klasifikovaných dat použijte funkci ppatterns.
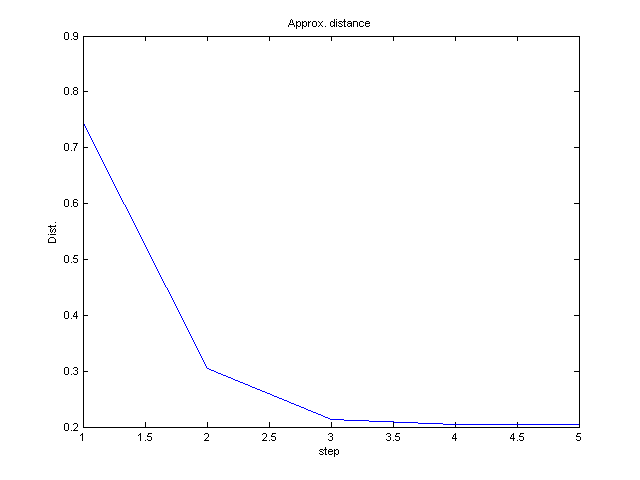
  3. V každé iteraci vykreslujte střední vzdálenost bodů k nejblizšímu μj.
  4. Zkuste různé hodnoty K , např. K = 2,3,4. Algoritmus spouštějte opakovaně, iniciální hodnoty μj volte náhodně pomocí funkce rand.
Úkázka možného výsledku:
klasifkace klasifkace

Část 2: Odhad parametrů gaussovské směsi

Algoritmus K-means nyní použijeme pro odhad parametrů gaussovské směsi. Předpokládejme, že distribuce dat odpovídá směsi 3 normálních rozdělení (gaussiánů)

p(x) = Sum3j=1 P(j) N( x | μj , Σj) ,

kde N(μj , Σj) značí normální rozdělení se střední hodnotou μ j a kovariancí Σ j a P(j) značí váhu příslušného gaussiánu. Cílem úlohy je na základě naměřených vstupních dat x1 , x2 , ... , xN odhadnout parametry směsi μ j , Σ j , P(j).

Úkoly:
  1. V každé iteraci algoritmu K-means, po rozklasifikování vzorků, proveďte ML-odhad středních hodnot μ j a kovariancí Σ j .
    P(j)     vyčíslujte jako relativní četnost vzorků v j-tém shluku.

    Poznámka 1: Je třeba vědět, co to je maximálně věrohodný (ML) odhad. Viz patřičné cvičení.
    Poznámka 2: Data si vygenerujte pomocí funkce gmmsamp().

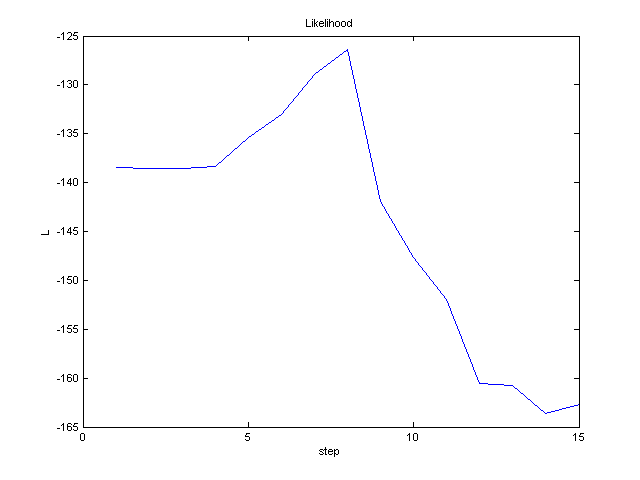
  2. Průběžně vykreslujte celkovou věrohodnost L odhadnutých parametrů μ j , Σ j , P(j) :

    L = log ΠNi=1 Sum3j=1 P(j) N(xi , μj , Σj)
    K vyčíslení věrohodnosti L gaussovské směsi můžete použít funkci likelihood (ke stažení zde: likelihood.m).

    Poznámka: Pokud pro výpočet věrohodnosti použijete zmíněnou funkci a ne vlastní, musíte být schopni vysvětli/odvodit výše uvedený vztah pro věrohodnost gaussovské směsi.
    3. likelihood
  3. Hledá metoda K-means maximálně věrohodný odhad parametrů?

Část 3: Učení bez učitele

Algoritmus K-means nyní vyzkoušíme v úloze "učení bez učitele". Na vstupu máme neoznačenou sadu obrázků třech písmen H, L, T. Cílem úlohy je sadu obrázku pomocí algoritmu K-means rozklasifikovat do tří tříd. Pro řešení budeme používat obvyklých dvou obrazových měření:
x = (součet hodnot pixelů v levé polovině obrázku) - (součet hodnot pixelů v pravé polovině obrázku)
y = (součet hodnot pixelů v horní polovině obrázku) - (součet hodnot pixelů v dolní polovině obrázku)
Úkoly:
  1. Nahrajte si vstupni sadu obrázků image_data.mat.
  2. Pomocí K-means rozklasifikujte sadu do třech tříd. V každé iteraci opět vykreslujte μj , klasifikaci, a věrohodnost L .
  3. Po ukončení algoritmu spočtěte průměrný obrázek každé nalezené třídy, výsledek zobrazte. K ověření/zobrazení výsledků klasifikace můžete také využít funkci show_class (viz. show_class.m).
  4. Rozumíte, proč se úloze říká "učení bez učitele"?
Ukázka možných výsledků:
Třída 1Třída 2Třída 3
klasifkace klasifkace klasifkace

Doporučená literatura

[1] Podklady pro cvičení (2005)

Created by Martin Urban, last update 10.12.2008