Central Panoramic Cameras.

Tomas Svoboda, Tomas Pajdla, and Vaclav Hlavac

Keywords: computer vision, omnidirectional vision, epipolar geometry, panoramic cameras, hyperbolic mirror, stereo

Introduction

This page gives the foundations of panoramic stereo vision by presenting the analysis of epipolar geometry for panoramic cameras. The panoramic cameras with convex hyperbolic or parabolic mirror, so called central panoramic cameras, allow the epipolar geometry as perspective cameras.

Motivation

Using standard perspective (pinhole) cameras the motion estimation algorithm cannot, in some cases, well distinguish a small pure translation of the camera from a small rotation. The confusion can be removed if a camera with large field of view is used. Ideally one would like to use a panoramic camera which has complete 360° field of view and sees to all directions. It can be imagined as a pinhole camera with a spherical imaging surface (instead of planar one as it is usual) centered at the focal point of the pinhole camera. Panoramic camera can, in principle, obtain correspondences from everywhere independently of the direction of motion.

Problems to be solved

Motion estimation from panoramic images requires to:

design a practical panoramic camera with simple mathematical model and propose method for its calibration,
develop the epipolar geometry for panoramic images, and
work out an algorithm for motion estimation.

Panoramic stereo vision also needs efficient search for the correspondences in panoramic images which calls for:

the analysis of the shape of the epipolar curves in order to constraint the locations of corresponding points and for
the study of epipolar alignment of the panoramic images in order to speed up the search.

Design of the mirror

We do not consider here panoramic vision systems with moving parts since they are not applicable for real time imaging. The panoramic camera covering almost the whole imaging sphere can be obtained by combining a classical perspective (pinhole) camera with a convex mirror.

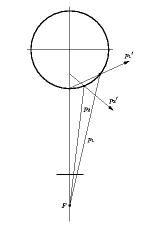
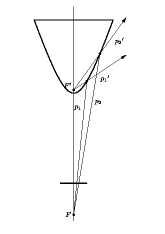
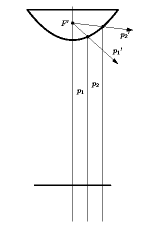
Spherical mirror. The reflected optical rays do not intersect in a unique point. Spherical aberration. Hyperbolic mirror. The reflected optical rays intersect in the focus of the hyperboloid. The center of camera projection coincides with the second mirror focus. Parabolic mirror. The reflected optical rays intersect in the focus of the paraboloid when orthographic projection is assumed. The second mirror focus goes to the infinity.
Next we focus on the case when all reflected rays intersect at a single point. Panoramic cameras which possess this property shall be called central panoramic cameras. Theses cameras allow the epipolar geometry as perspective cameras.

Epipolar Geometry

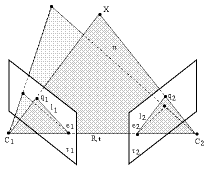Epipolar geometry geometry of two perspective cameras assigns to each point q₁ in one image an epipolar line l₂ in the second image. The mathematical expression of the epipolar geometry is

q₂^T Q q₁ = 0, where Q represents 3x3 fundamental matrix. The question arises what is the shape of the epipolar curves for central panoramic cameras.

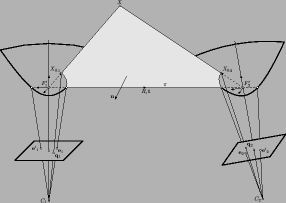Each epipolar plane intersects the mirror in a planar conic. To a point q₁ in the first image a conic in the second image

q₂^T A₂(E,q₁) q₂ = 0 is assigned. The matrix A₂(E,q₁) is in general case a nonlinear function of motion parameters R, t, point q₁, and the calibration parameters of the panoramic cameras and the mirrors.

Experiments with real sensor.

Back to Omnidir main page.


Spherical mirror. The reflected optical rays do not intersect in a unique point. Spherical aberration.	Hyperbolic mirror. The reflected optical rays intersect in the focus of the hyperboloid. The center of camera projection coincides with the second mirror focus.	Parabolic mirror. The reflected optical rays intersect in the focus of the paraboloid when orthographic projection is assumed. The second mirror focus goes to the infinity.