Coherence

A function related to cross-correlation is the coherence function, defined in terms of power spectral densities and the cross-spectral density by

$$\Gamma_{xy}(\omega) \isdef \frac{R_{xy}(\omega)}{\sqrt{R_x(\omega)R_y(\omega)}}.$$

In practice, these quantities can be estimated by averaging $\overline{X(\omega_k)}Y(\omega_k)$, $\left\vert X(\omega_k)\right\vert^2$, and $\left\vert Y(\omega_k)\right\vert^2$ over successive signal blocks. Let $\{\cdot\}_m$ denote time averaging across frames as in Eq. (8.3) above. Then an estimate of the coherence, the sample coherence function ${\hat\Gamma}_{xy}(\omega_k)$, may be defined by

$${\hat\Gamma}_{xy}(\omega_k) \isdef \frac{\left\{\overline{X_m(\o... ...vert^2\right\}_m\cdot\left\{\left\vert Y_m(\omega_k)\right\vert^2\right\}_m}}.$$

The magnitude-squared coherence $\left\vert\Gamma_{xy}(\omega)\right\vert^2$ is a real function between zero and one which gives a measure of correlation between $x$ and $y$ at each frequency $\omega$. For example, imagine that $y$ is produced from $x$ via an LTI filtering operation:

$$y = h\ast x \;\implies\; Y(\omega_k) = H(\omega_k)X(\omega_k)$$

Then the sample coherence function in each frame is

$$\begin{eqnarray*} {\hat \Gamma}_{x_my_m}(\omega_k) &\isdef & \frac{\overline{X_m... ...ht\vert} = \frac{H(\omega_k)}{\left\vert H(\omega_k)\right\vert} \end{eqnarray*}$$

and the magnitude-squared sample coherence function is simply

$$\left\vert{\hat \Gamma}_{xy}(\omega_k)\right\vert^2 = \left\vert\frac{H(\omega_k)}{\left\vert H(\omega_k)\right\vert}\right\vert^2 = 1.$$

On the other hand, when $x$ and $y$ are uncorrelated (e.g., $y$ is a noise process not derived from $x$), the sample coherence converges to zero at all frequencies, as the number of blocks $M$ goes to infinity.

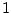A common use for the coherence function is in the validation of input/output data collected in an acoustics experiment for purposes of system identification. For example, $x(n)$ might be a known signal which is input to an unknown system, such as a reverberant room, say, and $y(n)$ is the recorded response of the room. Ideally, the coherence should be $1$ at all frequencies. However, if the microphone is situated at a null in the room response for some frequency, it may record mostly noise at that frequency. This is indicated in the measured coherence by a significant dip below 1.