The DFT and its Inverse Restated

Let $x(n), n=0,1,2,\ldots,N-1$, denote an $N$-sample complex sequence, i.e., $x\in{\bf C}^N$. Then the spectrum of $x$ is defined by the Discrete Fourier Transform (DFT):

$$\zbox {X(k) \isdef \sum_{n=0}^{N-1}x(n) e^{-j 2\pi nk/N},\quad k=0,1,2,\ldots,N-1}$$

The inverse DFT (IDFT) is defined by

$$\zbox {x(n) = \frac{1}{N}\sum_{k=0}^{N-1}X(k) e^{j 2\pi nk/N},\quad n=0,1,2,\ldots,N-1.}$$

Note that for the first time we are not carrying along the sampling interval $T=1/f_s$ in our notation. This is actually the most typical treatment in the digital signal processing literature. It is often said that the sampling frequency is $f_s=1$. However, it can be set to any desired value using the substitution

$$e^{j 2\pi nk/N} = e^{j 2\pi k (f_s/N) nT} \isdef e^{j \omega_k t_n}.$$

However, for the remainder of this chapter, we will adopt the more common (and more mathematical) convention $f_s=1$. In particular, we'll use the definition $\omega_k \isdef 2\pi k/N$ for this chapter only. 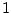In this case, a radian frequency $\omega_k$ is in units of ``radians per sample.'' Elsewhere in this book, $\omega_k$ always means ``radians per second.'' (Of course, there's no difference when the sampling rate is really $1$.) Another term we use in connection with the $f_s=1$ convention is normalized frequency: All normalized radian frequencies lie in the range $[-\pi,\pi)$, and all normalized frequencies in Hz lie in the range $[-0.5,0.5)$.