



Next: Orienting epipolar lines
Up: Epipolar geometry
Previous: Epipolar geometry
Contents
The transfer of corresponding epipolar lines is described by the following equations:
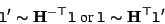 |
(G2) |
with  a homography for an arbitrary plane. As seen in [103] a valid homography can be obtained immediately from the fundamental matrix:
a homography for an arbitrary plane. As seen in [103] a valid homography can be obtained immediately from the fundamental matrix:
![\begin{displaymath}
{\bf H} = [{\tt e'}]_\times {\bf F} + {\tt e}'{\tt a}^\top
\end{displaymath}](img725.gif) |
(G3) |
with 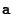 a random vector for which det
a random vector for which det
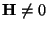 so that
so that  is invertible.
If one disposes of camera projection matrices an alternative homography is easily obtained as:
is invertible.
If one disposes of camera projection matrices an alternative homography is easily obtained as:
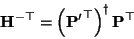 |
(G4) |
where  indicates the Moore-Penrose pseudo inverse.
indicates the Moore-Penrose pseudo inverse.
Marc Pollefeys
2000-07-12