



Next: Seven-point algorithm
Up: Two view geometry computation
Previous: Two view geometry computation
Contents
The two view structure is equivalent to the fundamental matrix. Since the fundamental matrix 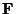 is a
is a  matrix determined up to an arbitrary scale factor, 8 equations are required to obtain a unique solution. The simplest way to compute the fundamental matrix consists of using Equation (3.26). This equation can be rewritten under the following form:
matrix determined up to an arbitrary scale factor, 8 equations are required to obtain a unique solution. The simplest way to compute the fundamental matrix consists of using Equation (3.26). This equation can be rewritten under the following form:
![\begin{displaymath}
\left[ \begin{array}{ccccccccc}
x x' & y x' & x' & x y' & y y' & y' & x & y & 1 \end{array} \right]
{\bf f} = 0
\end{displaymath}](img476.gif) |
(D6) |
with
![${\tt m}=[x \, y \, 1]^\top,{\tt m'}=[x' y' 1]^\top$](img477.gif) and
and
![${\bf f}=[F_{11} F_{12} F_{13} F_{21} F_{22} F_{23} F_{31} F_{32} F_{33} ]^\top$](img478.gif) a vector containing the elements of the fundamental matrix
a vector containing the elements of the fundamental matrix 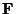 . By stacking eight of these equations in a matrix
. By stacking eight of these equations in a matrix  the following equation is obtained:
the following equation is obtained:
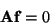 |
(D7) |
This system of equation is easily solved by Singular Value Decomposition (SVD) [58]. Applying SVD to  yields the decomposition
yields the decomposition
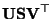 with
with 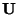 and
and  orthonormal matrices and
orthonormal matrices and 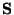 a diagonal matrix containing the singular values. These singular values
a diagonal matrix containing the singular values. These singular values 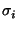 are positive and in decreasing order. Therefore in our case
are positive and in decreasing order. Therefore in our case 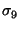 is guaranteed to be identically zero (8 equations for 9 unknowns) and thus the last column of
is guaranteed to be identically zero (8 equations for 9 unknowns) and thus the last column of  is the correct solution (at least as long as the eight equations are linearly independent, which is equivalent to all other singular values being non-zero).
is the correct solution (at least as long as the eight equations are linearly independent, which is equivalent to all other singular values being non-zero).
It is trivial to reconstruct the fundamental matrix 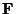 from the solution vector
from the solution vector 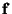 . However, in the presence of noise, this matrix will not satisfy the rank-2 constraint. This means that there will not be real epipoles through which all epipolar lines pass, but that these will be ``smeared out'' to a small region.
A solution to this problem is to obtain
. However, in the presence of noise, this matrix will not satisfy the rank-2 constraint. This means that there will not be real epipoles through which all epipolar lines pass, but that these will be ``smeared out'' to a small region.
A solution to this problem is to obtain 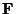 as the closest rank-2 approximation of the solution coming out of the linear equations.
as the closest rank-2 approximation of the solution coming out of the linear equations.




Next: Seven-point algorithm
Up: Two view geometry computation
Previous: Two view geometry computation
Contents
Marc Pollefeys
2000-07-12
![]() is a
is a ![]() matrix determined up to an arbitrary scale factor, 8 equations are required to obtain a unique solution. The simplest way to compute the fundamental matrix consists of using Equation (3.26). This equation can be rewritten under the following form:
matrix determined up to an arbitrary scale factor, 8 equations are required to obtain a unique solution. The simplest way to compute the fundamental matrix consists of using Equation (3.26). This equation can be rewritten under the following form:
![]() from the solution vector
from the solution vector ![]() . However, in the presence of noise, this matrix will not satisfy the rank-2 constraint. This means that there will not be real epipoles through which all epipolar lines pass, but that these will be ``smeared out'' to a small region.
A solution to this problem is to obtain
. However, in the presence of noise, this matrix will not satisfy the rank-2 constraint. This means that there will not be real epipoles through which all epipolar lines pass, but that these will be ``smeared out'' to a small region.
A solution to this problem is to obtain ![]() as the closest rank-2 approximation of the solution coming out of the linear equations.
as the closest rank-2 approximation of the solution coming out of the linear equations.