



Next: Relation between the fundamental
Up: Multi view geometry
Previous: Multi view geometry
Contents
Two view geometry
In this section the following question will be addressed: Given an image point in one image, does this restrict the position of the corresponding image point in another image? It turns out that it does and that this relationship can be obtained from the calibration or even from a set of prior point correspondences.
Although the exact position of the scene point  is not known, it is bound to be on the line of sight of the corresponding image point
is not known, it is bound to be on the line of sight of the corresponding image point 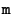 . This line can be projected in another image and the corresponding point
. This line can be projected in another image and the corresponding point  is bound to be on this projected line
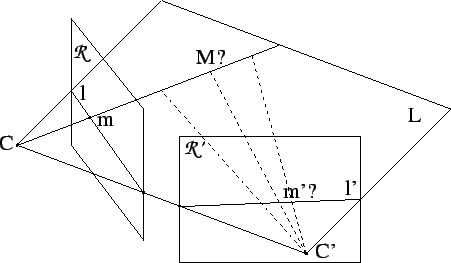
is bound to be on this projected line 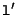 . This is illustrated in Figure 3.5.
. This is illustrated in Figure 3.5.
Figure 3.5:
Correspondence between two views. Even when the exact position of the 3D point  corresponding to the image point
corresponding to the image point  is not known, it has to be on the line through
is not known, it has to be on the line through 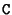 which intersects the image plane in
which intersects the image plane in  . Since this line projects to the line
. Since this line projects to the line 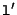 in the other image, the corresponding point
in the other image, the corresponding point  should be located on this line. More generally, all the points located on the plane defined by
should be located on this line. More generally, all the points located on the plane defined by 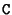 ,
, 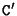 and
and  have their projection on
have their projection on 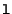 and
and 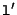 .
.
 |
In fact all the points on the plane  defined by the two projection centers and
defined by the two projection centers and  have their image on
have their image on  . Similarly, all these points are projected on a line
. Similarly, all these points are projected on a line  in the first image.
in the first image.
 and
and  are said to be in epipolar correspondence (i.e. the corresponding point of every point on
are said to be in epipolar correspondence (i.e. the corresponding point of every point on  is located on
is located on 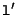 , and vice versa).
, and vice versa).
Every plane passing through both centers of projection  and
and 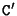 results in such a set of corresponding epipolar lines, as can be seen in Figure 3.6. All these lines pass through two specific points
results in such a set of corresponding epipolar lines, as can be seen in Figure 3.6. All these lines pass through two specific points 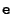 and
and 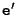 . These points are called the epipoles, and they are the projection of the center of projection in the opposite image.
. These points are called the epipoles, and they are the projection of the center of projection in the opposite image.
Figure 3.6:
Epipolar geometry. The line connecting 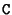 and
and 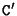 defines a bundle of planes. For every one of these planes a corresponding line can be found in each image, e.g. for
defines a bundle of planes. For every one of these planes a corresponding line can be found in each image, e.g. for  these are
these are 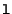 and
and 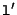 . All 3D points located in
. All 3D points located in  project on
project on 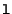 and
and 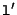 and thus all points on
and thus all points on 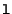 have their corresponding point on
have their corresponding point on 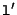 and vice versa. These lines are said to be in epipolar correspondence. All these epipolar lines must pass through
and vice versa. These lines are said to be in epipolar correspondence. All these epipolar lines must pass through 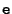 or
or 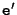 , which are the intersection points of the line
, which are the intersection points of the line 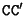 with the retinal planes
with the retinal planes  and
and 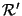 respectively. These points are called the epipoles.
respectively. These points are called the epipoles.
 |
This epipolar geometry can also be expressed mathematically. The fact that a point 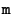 is on a line
is on a line  can be expressed as
can be expressed as
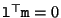 . The line passing trough
. The line passing trough 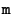 and the epipole
and the epipole 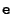 is
is
![\begin{displaymath}
{\tt l} \sim [{\tt e}]_\times {\tt m} \, ,
\end{displaymath}](img401.gif) |
(C23) |
with
![$[{\tt e}]_\times$](img402.gif) the antisymmetric
the antisymmetric  matrix representing the vectorial product with
matrix representing the vectorial product with 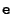 .
.
From (3.9) the plane 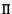 corresponding to
corresponding to  is easily obtained as
is easily obtained as
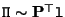 and similarly
and similarly
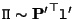 . Combining these equations gives:
. Combining these equations gives:
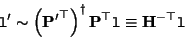 |
(C24) |
with  indicating the Moore-Penrose pseudo-inverse. The notation
indicating the Moore-Penrose pseudo-inverse. The notation
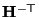 is inspired by equation (2.7). Substituting (3.23) in (3.24) results in
is inspired by equation (2.7). Substituting (3.23) in (3.24) results in
Defining
![${\bf F} = {\bf H}^{-\top} [{\tt e}]_\times$](img409.gif) , we obtain
, we obtain
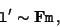 |
(C25) |
and thus,
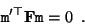 |
(C26) |
This matrix 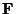 is called the fundamental matrix. These concepts were introduced by Faugeras [44] and Hartley [60]. Since then many people have studied the properties of this matrix (e.g. [102,103]) and a lot of effort has been put in robustly obtaining this matrix from a pair of uncalibrated images [195,196,225].
is called the fundamental matrix. These concepts were introduced by Faugeras [44] and Hartley [60]. Since then many people have studied the properties of this matrix (e.g. [102,103]) and a lot of effort has been put in robustly obtaining this matrix from a pair of uncalibrated images [195,196,225].
Having the calibration, 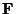 can be computed and a constraint is obtained for corresponding points. When the calibration is not known equation (3.26) can be used to compute the fundamental matrix
can be computed and a constraint is obtained for corresponding points. When the calibration is not known equation (3.26) can be used to compute the fundamental matrix 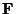 . Every pair of corresponding points gives one constraint on
. Every pair of corresponding points gives one constraint on 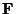 . Since
. Since 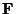 is a
is a  matrix which is only determined up to scale, it has
matrix which is only determined up to scale, it has
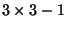 unknowns. Therefore 8 pairs of corresponding points are sufficient to compute
unknowns. Therefore 8 pairs of corresponding points are sufficient to compute 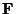 with a linear algorithm.
with a linear algorithm.
Note from (3.25) that
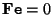 , because
, because
![$[{\tt e}]_\times {\tt e} = 0$](img414.gif) . Thus,
. Thus,
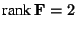 . This is an additional constraint on
. This is an additional constraint on 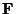 and therefore 7 point correspondences are sufficient to compute
and therefore 7 point correspondences are sufficient to compute 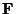 through a nonlinear algorithm.
In Section 4.3 the robust computation of the fundamental matrix from images will be discussed in more detail.
through a nonlinear algorithm.
In Section 4.3 the robust computation of the fundamental matrix from images will be discussed in more detail.
Subsections




Next: Relation between the fundamental
Up: Multi view geometry
Previous: Multi view geometry
Contents
Marc Pollefeys
2000-07-12
![]() is not known, it is bound to be on the line of sight of the corresponding image point
is not known, it is bound to be on the line of sight of the corresponding image point ![]() . This line can be projected in another image and the corresponding point
. This line can be projected in another image and the corresponding point ![]() is bound to be on this projected line
is bound to be on this projected line ![]() . This is illustrated in Figure 3.5.
. This is illustrated in Figure 3.5.

![]() and
and ![]() results in such a set of corresponding epipolar lines, as can be seen in Figure 3.6. All these lines pass through two specific points
results in such a set of corresponding epipolar lines, as can be seen in Figure 3.6. All these lines pass through two specific points ![]() and
and ![]() . These points are called the epipoles, and they are the projection of the center of projection in the opposite image.
. These points are called the epipoles, and they are the projection of the center of projection in the opposite image.

![]() is on a line
is on a line ![]() can be expressed as
can be expressed as
![]() . The line passing trough
. The line passing trough ![]() and the epipole
and the epipole ![]() is
is
![]() corresponding to
corresponding to ![]() is easily obtained as
is easily obtained as
![]() and similarly
and similarly
![]() . Combining these equations gives:
. Combining these equations gives:
![]() can be computed and a constraint is obtained for corresponding points. When the calibration is not known equation (3.26) can be used to compute the fundamental matrix
can be computed and a constraint is obtained for corresponding points. When the calibration is not known equation (3.26) can be used to compute the fundamental matrix ![]() . Every pair of corresponding points gives one constraint on
. Every pair of corresponding points gives one constraint on ![]() . Since
. Since ![]() is a
is a ![]() matrix which is only determined up to scale, it has
matrix which is only determined up to scale, it has
![]() unknowns. Therefore 8 pairs of corresponding points are sufficient to compute
unknowns. Therefore 8 pairs of corresponding points are sufficient to compute ![]() with a linear algorithm.
with a linear algorithm.
![]() , because
, because
![]() . Thus,
. Thus,
![]() . This is an additional constraint on
. This is an additional constraint on ![]() and therefore 7 point correspondences are sufficient to compute
and therefore 7 point correspondences are sufficient to compute ![]() through a nonlinear algorithm.
In Section 4.3 the robust computation of the fundamental matrix from images will be discussed in more detail.
through a nonlinear algorithm.
In Section 4.3 the robust computation of the fundamental matrix from images will be discussed in more detail.