Subsections
Let the analyzed object (texture in our case) be described by two
random variables 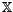 and
and 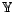 which are assumed to have a probability
distribution function
which are assumed to have a probability
distribution function
The distribution is known up to its parameter(s)
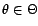 .
It is assumed that we are given a set of samples
.
It is assumed that we are given a set of samples
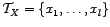 independently drawn from the distribution
independently drawn from the distribution
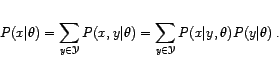 |
(1) |
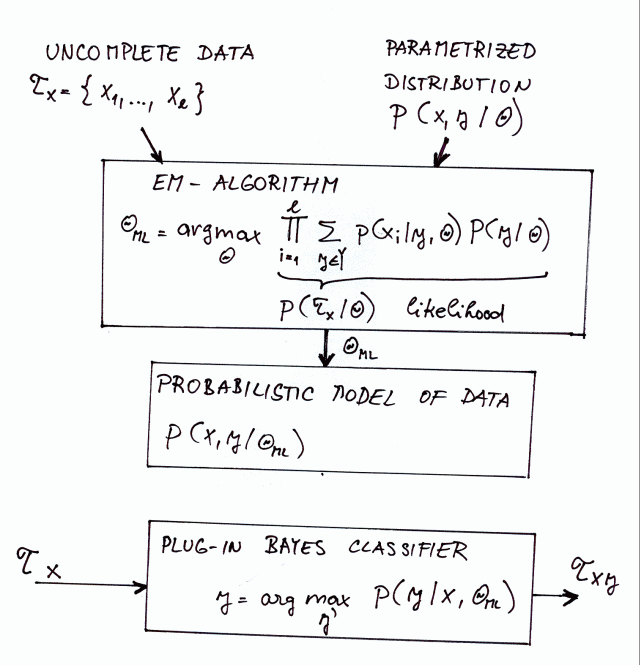
The Expectation-Maximization (EM) algorithm is an optimization procedure which
computes the Maximal-Likelihood (ML) estimate of the unknown parameter
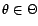 when only uncomplete (
when only uncomplete (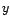 is unknown) data
is unknown) data 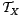 are
presented. In other words, the EM algorithm maximizes the likelihood
function
are
presented. In other words, the EM algorithm maximizes the likelihood
function
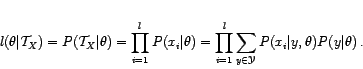 |
(2) |
with respect to the parameter
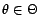 .
.
A particular example of the distribution (1) which can be
estimated by the EM algorithm is the Gaussian Mixture Model (GMM). In this
case the distribution 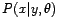 is the multi-variate Gaussian distribution
is the multi-variate Gaussian distribution
The random variable 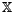 attains value from the set
attains value from the set
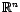 and the variable
and the variable
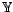 from a discrete set
from a discrete set
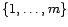 . The unknown parameter consists of
mean vectors
. The unknown parameter consists of
mean vectors 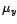 ,
, 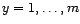 , covariance matrices
, covariance matrices 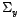 ,
,
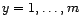 and values of the discrete distribution
and values of the discrete distribution 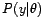 . The number
. The number
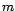 of the Gaussian components must be prescribed before the EM is applied. For
instance, the cross-validation can be used to select the proper
of the Gaussian components must be prescribed before the EM is applied. For
instance, the cross-validation can be used to select the proper 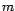 . This
involves maximization of the cross-validation estimate of the likelihood
function (2) with respect to
. This
involves maximization of the cross-validation estimate of the likelihood
function (2) with respect to 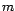 .
.
The estimated GMM can be used for data clustering. In this case it is assumed
that the similar data which belong to one cluster (class) are generated
by an identical Gaussian component. The value of the random variable 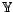 then
identifies the corresponding cluster. The whole clustering procedure involves:
then
identifies the corresponding cluster. The whole clustering procedure involves:
- Estimation of the GMM model by the EM algorithm.
- Classification of the data to classes based on the estimated
model (1). The Bayesian classifier is naturally used to
classify the data.
Figure 3:
Expectation-Maximization Algorithm for clustering.
 |
- Implement the cross-validation procedure for tuning the number
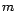 of
Gaussian components in the GMM estimated by the EM algorithm.
of
Gaussian components in the GMM estimated by the EM algorithm.
- Apply the cross-validation procedure to cluster unlabeled data made
from the Brodatz textures
[brodatz2_trn.mat].
estimate of the likelihood function with respect to the number of
components
 .
.
- Validate the result of clustering by visual inspection.
| em_exp1 |
Example on using EM
algorithm. |
| crossval |
Partitions data for cross-validation. |
| emgmm |
EM algorithm for the Gaussian Mixture Model. |
| pdfgmm |
Evaluates GMM distribution function. |
Vojtech Franc
2004-08-31
![]() and
and ![]() which are assumed to have a probability
distribution function
which are assumed to have a probability
distribution function
![]() is the multi-variate Gaussian distribution
is the multi-variate Gaussian distribution
![]() then
identifies the corresponding cluster. The whole clustering procedure involves:
then
identifies the corresponding cluster. The whole clustering procedure involves: