Initial frame

The two first images of the sequence are used to determine a reference frame. The world frame is aligned with the first camera. The second camera is chosen so that the epipolar geometry corresponds to the retrieved ${\bf F}_{12}$ (see equation 3.30).

$$\begin{array}{rcrcccl} {\bf P}_1 &=& [ & {\bf I}_{3 \times 3... ..._{12} {\tt\pi}^\top &\vert& \sigma {\tt e}_{12} & ] \end{array}$$ (E1)

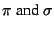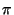where $[{\tt e}_{12}]_\times$ indicates the vector product with ${\tt e}_{12}$. Equation 5.1 is not completely determined by the epipolar geometry (i.e. ${\bf F}_{12}$ and ${\tt e}_{12}$), but has 4 more degrees of freedom (i.e. ${\tt\pi} \mbox{ and } \sigma$). ${\tt\pi}$ determines the position of the reference plane (i.e. the plane at infinity in an affine or metric frame) and $\sigma$ determines the global scale of the reconstruction. The parameter $\sigma$ can simply be put to one or alternatively the baseline between the two initial views can be scaled to one.

Determining suitable values for 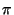${\tt\pi}$ is less obvious. Although strictly speaking at this level only the projective structure will be recovered, several steps are simplified if one can assume that the projective skew is not too large. In this case measurements in space can at least be used qualitatively. How this can be achieved is explained in the following section.