



Next: Initialize new structure
Up: Adding a view
Previous: projective pose estimation
Contents
The structure is refined using an Iterated Extended Kalman Filter for each point. The notation 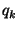 is used to indicate a quantity
is used to indicate a quantity 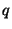 in view
in view 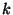 , and
, and  to indicate a estimation based on the observations up to view
to indicate a estimation based on the observations up to view 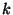 . The observation equation is:
. The observation equation is:
![\begin{displaymath}
\left[ \begin{array}{c} x_k \\ y_k \end{array} \right] =
{\t...
...tt M} \\ {\tt P}_{k2} {\tt M}
\end{array} \right] + {\tt w}_k
\end{displaymath}](img536.gif) |
(E4) |
where  and
and  are the image coordinates of the observed feature,
are the image coordinates of the observed feature,  is the observed 3D point and
is the observed 3D point and 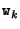 is zero-mean Gaussian noise (uncorrelated over the images).
is zero-mean Gaussian noise (uncorrelated over the images). 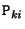 is the
is the 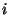 th row of the projection matrix
th row of the projection matrix 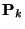 . The update equations for state vector and covariance matrix are
. The update equations for state vector and covariance matrix are
where the Kalman gain matrix, innovation vector, and innovation covariance are
respectively, and 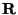 is the covariance matrix for the observed image points
is the covariance matrix for the observed image points 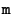 . The Jacobian
. The Jacobian
 of the non-linear observation equation 5.4 is evaluated at
of the non-linear observation equation 5.4 is evaluated at
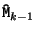
![\begin{displaymath}
\nabla {\tt p}_{\tt M} = \left[ \begin{array}{ccc}
\frac{\p...
...rtial Y} & \frac{\partial p_y}{\partial Z}
\end{array}\right]
\end{displaymath}](img553.gif) |
(E10) |
whose  -th element is
-th element is
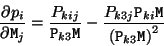 |
(E11) |
Within an IEKF, the update cycle in equations 5.5 and 5.6 is repeated for a number of iterations with
 evaluated at the current value of
evaluated at the current value of
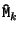 on each iteration. Beardsley et al [9] proposed 3 iterations.
on each iteration. Beardsley et al [9] proposed 3 iterations.
If a 3D point is not observed the position is not updated. In this case one can check if the point was seen in a sufficient number of views to be kept in the final reconstruction. This minimum number of views can for example be put to three. This avoids to have an important number of outliers due to spurious matches.




Next: Initialize new structure
Up: Adding a view
Previous: projective pose estimation
Contents
Marc Pollefeys
2000-07-12
![]() is used to indicate a quantity
is used to indicate a quantity ![]() in view
in view ![]() , and
, and ![]() to indicate a estimation based on the observations up to view
to indicate a estimation based on the observations up to view ![]() . The observation equation is:
. The observation equation is:
![$\displaystyle \left[ \begin{array}{c} x_k \\ y_k \end{array} \right]
- {\tt p}\left( {\tt\hat{M}}_{k-1} \right)$](img548.gif)