



Next: Levenberg-Marquardt iteration
Up: Levenberg-Marquardt minimization
Previous: Levenberg-Marquardt minimization
Contents
Newton's approach starts from an initial value 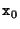 and refines this value using the assumption that
and refines this value using the assumption that 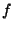 is locally linear. A first order approximation of
is locally linear. A first order approximation of
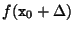 yields:
yields:
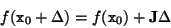 |
(E13) |
with 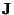 the Jacobian matrix and
the Jacobian matrix and 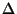 a small displacement. Under these assumptions minimizing
a small displacement. Under these assumptions minimizing
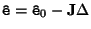 can be solved through linear least-squares. A simple derivation yields
can be solved through linear least-squares. A simple derivation yields
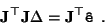 |
(E14) |
This equation is called the normal equation. The solution to the problem is found by starting from an initial solution and refining it based on successive iterations
 |
(E15) |
with 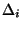 the solution of the normal equation 5.14 evaluated at
the solution of the normal equation 5.14 evaluated at 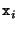 . One hopes that this algorithm will converge to the desired solution, but it could also end up in a local minimum or not converge at all. This depends a lot on the initial value
. One hopes that this algorithm will converge to the desired solution, but it could also end up in a local minimum or not converge at all. This depends a lot on the initial value 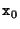 .
.




Next: Levenberg-Marquardt iteration
Up: Levenberg-Marquardt minimization
Previous: Levenberg-Marquardt minimization
Contents
Marc Pollefeys
2000-07-12