 Why Exponentials are Important
Why Exponentials are Important
 Constructive and Destructive Interference
Constructive and Destructive Interference
 Sinusoids and Exponentials
Contents
Global Contents
Sinusoids and Exponentials
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
The canonical form of an exponential function, as typically used in signal
processing, is
where  is called the time constant of the exponential.
is called the time constant of the exponential. 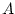 is
the peak amplitude, as before. The time constant is the time it takes to decay
by
is
the peak amplitude, as before. The time constant is the time it takes to decay
by  , i.e.,
A normalized exponential decay is depicted in Fig. 4.5.
, i.e.,
A normalized exponential decay is depicted in Fig. 4.5.
Figure:
The decaying exponential
 .
.
 |
Subsections
 Why Exponentials are Important
Why Exponentials are Important
 Constructive and Destructive Interference
Constructive and Destructive Interference
 Sinusoids and Exponentials
Contents
Global Contents
Sinusoids and Exponentials
Contents
Global Contents
 Global Index
Index
Search
Global Index
Index
Search
``Mathematics of the Discrete Fourier Transform (DFT)'',
by Julius O. Smith III,
W3K Publishing, 2003, ISBN 0-9745607-0-7.
(Browser settings for best viewing results)
(How to cite this work)
(Order a printed hardcopy)
Copyright © 2003-10-09 by Julius O. Smith III
Center for Computer Research in Music and Acoustics (CCRMA),
Stanford University
 (automatic links disclaimer)
(automatic links disclaimer)
