



Next: Deviations from the camera
Up: The projection matrix
Previous: The projection matrix
Contents
The homographies that will be discussed here are collineations from
 . A homography
. A homography  describes the transformation from one plane to another. A number of special cases are of interest, since the image is also a plane. The projection of points of a plane into an image
describes the transformation from one plane to another. A number of special cases are of interest, since the image is also a plane. The projection of points of a plane into an image 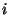 can be described through a homography
can be described through a homography
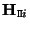 . The matrix representation of this homography is dependent on the choice of the projective basis in the plane.
. The matrix representation of this homography is dependent on the choice of the projective basis in the plane.
As an image is obtained by perspective projection, the relation between points
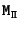 belonging to a plane
belonging to a plane 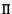 in 3D space and their projections
in 3D space and their projections
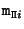 in the image is mathematically expressed by a homography
in the image is mathematically expressed by a homography
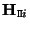 . The matrix of this homography is found as follows. If the plane
. The matrix of this homography is found as follows. If the plane 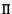 is given by
is given by
![${\tt\Pi} \sim [{\tt\pi}^\top \, 1]^\top$](img336.gif) and the point
and the point
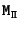 of
of 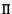 is represented as
is represented as
![${\tt M}_{\tt\Pi} \sim [{\tt m}^\top_{\tt\Pi} \, 1]^\top$](img337.gif) , then
, then
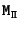 belongs to
belongs to 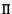 if and only if
if and only if
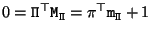 . Hence,
. Hence,
![\begin{displaymath}
{\tt M}_{\tt\Pi} \sim \left[ \begin{array}{c} {\tt m}_{\tt\P...
...{\tt\pi}^\top \end{array} \right] {\tt m}_{\tt\Pi}
\enspace .
\end{displaymath}](img339.gif) |
(C13) |
Now, if the camera projection matrix is
![${\bf P}_i=[{\bf A}_i \vert {\tt a}_i ]$](img340.gif) , then the projection
, then the projection
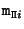 of
of
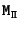 onto the image is
onto the image is
Consequently,
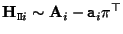 .
.
Note that for the specific plane
![${\tt\Pi}_{\tt REF}= [0\,0\,0\,1]^\top$](img346.gif) the homographies are simply given by
the homographies are simply given by
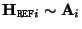 .
.
It is also possible to define homographies which describe the transfer from one image to the other for points and other geometric entities located on a specific plane. The notation
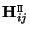 will be used to describe such a homography from view
will be used to describe such a homography from view 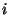 to
to 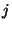 for a plane
for a plane 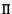 . These homographies can be obtained through the following relation
. These homographies can be obtained through the following relation
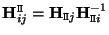 and are independent to reparameterizations of the plane (and thus also to a change of basis in
and are independent to reparameterizations of the plane (and thus also to a change of basis in  ).
).
In the metric and Euclidean case,
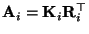 and the plane at infinity is
and the plane at infinity is
![${\tt\Pi}_\infty=[0 0 0 1]^\top$](img351.gif) . In this case, the homographies for the plane at infinity can thus be written as:
. In this case, the homographies for the plane at infinity can thus be written as:
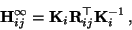 |
(C15) |
where
 is the rotation matrix that describes the relative orientation from the
is the rotation matrix that describes the relative orientation from the  camera with respect top the
camera with respect top the 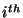 one.
one.
In the projective and affine case, one can assume that
![${\bf P}_1 = [{\bf I}_{3 \times 3} \vert {\tt0}_3]$](img356.gif) (since in this case
(since in this case  is unknown). In that case, the homographies
is unknown). In that case, the homographies
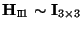 for all planes; and thus,
for all planes; and thus,
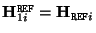 . Therefore
. Therefore  can be factorized as
can be factorized as
![\begin{displaymath}
{\bf P}_i = [ {\bf H}_{1i}^{\tt REF} \vert {\tt e}_{1i} ]
\end{displaymath}](img361.gif) |
(C16) |
where 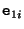 is the projection of the center of projection of the first camera (in this case,
is the projection of the center of projection of the first camera (in this case,
![$[0 \, 0\, 0\, 1]^\top$](img256.gif) ) in image
) in image 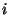 . This point
. This point 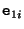 is called the epipole, for reasons which will become clear in Section 3.3.1.
is called the epipole, for reasons which will become clear in Section 3.3.1.
Note that this equation can be used to obtain
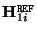 and
and 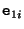 from
from  , but that due to the unknown relative scale factors
, but that due to the unknown relative scale factors  can, in general, not be obtained from
can, in general, not be obtained from
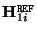 and
and 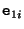 . Observe also that, in the affine case (where
. Observe also that, in the affine case (where
![${\tt\Pi}_\infty=[0 0 0 1]^\top$](img351.gif) ), this yields
), this yields
![${\bf P}_i = [ {\bf H}_{1i}^\infty \vert {\tt e}_{1i} ]$](img363.gif) .
.
Combining equations (3.14) and (3.16), one obtains
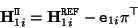 |
(C17) |
This equation gives an important relationship between the homographies for all possible planes. Homographies can only differ by a term
![${\tt e}_{1i} [{\tt l-\pi}']^\top$](img365.gif) .
This means that in the projective case the homographies for the plane at infinity are known up to 3 common parameters (i.e. the coefficients of
.
This means that in the projective case the homographies for the plane at infinity are known up to 3 common parameters (i.e. the coefficients of
 in the projective space).
in the projective space).
Equation (3.16) also leads to an interesting interpretation of the camera projection matrix:
In other words, a point can thus be parameterized as being on the line through the optical center of the first camera (i.e.
![$[0 0 0 1]^\top$](img371.gif) ) and a point in the reference plane
) and a point in the reference plane
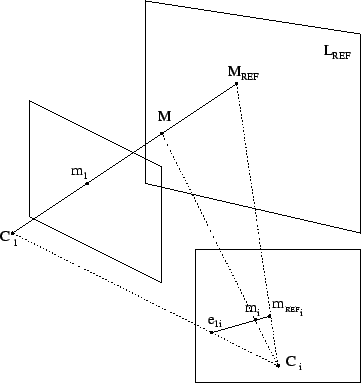
 . This interpretation is illustrated in Figure 3.4.
. This interpretation is illustrated in Figure 3.4.
Figure 3.4:
A point  can be parameterized as
can be parameterized as
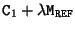 . Its projection in another image can then be obtained by transferring
. Its projection in another image can then be obtained by transferring 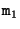 according to
according to
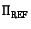 (i.e. with
(i.e. with
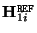 ) to image
) to image 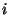 and applying the same linear combination with the projection
and applying the same linear combination with the projection  of
of 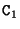 (i.e.
(i.e.
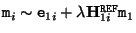 ).
).
 |




Next: Deviations from the camera
Up: The projection matrix
Previous: The projection matrix
Contents
Marc Pollefeys
2000-07-12
![]() belonging to a plane
belonging to a plane ![]() in 3D space and their projections
in 3D space and their projections
![]() in the image is mathematically expressed by a homography
in the image is mathematically expressed by a homography
![]() . The matrix of this homography is found as follows. If the plane
. The matrix of this homography is found as follows. If the plane ![]() is given by
is given by
![]() and the point
and the point
![]() of
of ![]() is represented as
is represented as
![]() , then
, then
![]() belongs to
belongs to ![]() if and only if
if and only if
![]() . Hence,
. Hence,
![]() the homographies are simply given by
the homographies are simply given by
![]() .
.
![]() will be used to describe such a homography from view
will be used to describe such a homography from view ![]() to
to ![]() for a plane
for a plane ![]() . These homographies can be obtained through the following relation
. These homographies can be obtained through the following relation
![]() and are independent to reparameterizations of the plane (and thus also to a change of basis in
and are independent to reparameterizations of the plane (and thus also to a change of basis in ![]() ).
).
![]() and the plane at infinity is
and the plane at infinity is
![]() . In this case, the homographies for the plane at infinity can thus be written as:
. In this case, the homographies for the plane at infinity can thus be written as:
![]() (since in this case
(since in this case ![]() is unknown). In that case, the homographies
is unknown). In that case, the homographies
![]() for all planes; and thus,
for all planes; and thus,
![]() . Therefore
. Therefore ![]() can be factorized as
can be factorized as
![]() and
and ![]() from
from ![]() , but that due to the unknown relative scale factors
, but that due to the unknown relative scale factors ![]() can, in general, not be obtained from
can, in general, not be obtained from
![]() and
and ![]() . Observe also that, in the affine case (where
. Observe also that, in the affine case (where
![]() ), this yields
), this yields
![]() .
.
![$\displaystyle [ {\bf I}_{3 \times 3} \vert {\tt0}_3] \left[\begin{array}{c} {\tt m} \\ 1 \end{array}\right] = {\tt m}$](img367.gif)
![$\displaystyle [ {\bf H}_{1i}^{\tt REF} \vert {\tt e}_{1i} ]
\left[\begin{array}...
...\tt m} \\ 1 \end{array}\right] = {\bf H}_{1i}^{\tt REF} {\tt m} + {\tt e}_{1i}$](img369.gif)
![$\displaystyle \lambda {\bf H}_{1i}^{\tt REF} {\tt m}_1 + {\tt e}_{1i} = {\bf P}...
...\end{array}\right] + \left[\begin{array}{c} {\tt0}_3 \\ 1 \end{array}\right] )$](img370.gif)
