



Next: Non-linear approach
Up: Flexible self-calibration
Previous: Flexible self-calibration
Contents
To obtain a linear algorithm based on equation (6.7) linear constraints on the dual image absolute conic are needed.
The problem is that the constraints are given in terms of intrinsic camera parameters which are squared in 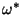 :
:
![\begin{displaymath}
\omega^* \sim {\bf KK}^\top \sim
\left[ \begin{array}{ccc} f...
... c_x c_y& f_y^2+c_y^2& c_y \\ c_x & c_y & 1 \end{array}\right]
\end{displaymath}](img661.gif) |
(F12) |
However, a known principal point yields two independent linear constraints on 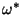 . If the principal point is known then a known skew also results in a linear constraint (i.e. by transforming the image so that the skew vanishes). If these three constraints are available, then a known focal length or aspect ratio also results in a linear constraint. Even if some of these constraints are only roughly satisfied this can be sufficient to provide a suitable initialization for the nonlinear method.
. If the principal point is known then a known skew also results in a linear constraint (i.e. by transforming the image so that the skew vanishes). If these three constraints are available, then a known focal length or aspect ratio also results in a linear constraint. Even if some of these constraints are only roughly satisfied this can be sufficient to provide a suitable initialization for the nonlinear method.
The set of constraints which is typically used for initialization consists of all intrinsics known but the focal length.
The constraints we impose simplify equation (6.7) as follows:
![\begin{displaymath}
\lambda
\left[ \begin{array}{ccc} f_i^2 & 0 & 0 \\
0 & f_i...
...\ c_4 & c_7 & c_9 & c_{10}
\end{array} \right]
{\bf P}_i^\top
\end{displaymath}](img662.gif) |
(F13) |
with  an explicit scale factor.
From the left-hand side of equation (6.13) it can be seen that the following equations have to be satisfied:
an explicit scale factor.
From the left-hand side of equation (6.13) it can be seen that the following equations have to be satisfied:
with
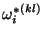 representing the element on row
representing the element on row 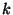 and column
and column  of
of 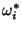 .
Note that due to symmetry (6.15) and (6.16) result in identical equations.
These constraints can thus be imposed on the right-hand side, yielding
.
Note that due to symmetry (6.15) and (6.16) result in identical equations.
These constraints can thus be imposed on the right-hand side, yielding 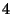 independent linear constraints in
independent linear constraints in
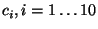 for every image:
for every image:
with 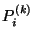 representing row
representing row 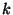 of
of  and
and  parameterized as in (6.13).
The rank 3 constraint can be imposed by taking the closest rank 3 approximation (using SVD for example). This approach holds for sequences of 3 or more images.
parameterized as in (6.13).
The rank 3 constraint can be imposed by taking the closest rank 3 approximation (using SVD for example). This approach holds for sequences of 3 or more images.
The special case of 2 images can also be dealt with, but with a slightly different approach. When only two views are available the solution is only determined up to a one parameter family of solutions
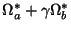 . Imposing the rank 3 constraint in this case should be done through the determinant:
. Imposing the rank 3 constraint in this case should be done through the determinant:
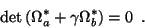 |
(F17) |
This results in up to 4 possible solutions. The constraint that the squared parameters should be positive can be used to eliminate some of these solutions. If more than one solution persists additional constraints should be used. These can come from knowledge about the camera (e.g. constant focal length) or about the scene (e.g. known angle).
The linear approach suffers from an additional critical motion sequence. This is caused by the fact that the planarity of the DAQ is only imposed a posteriori (closest rank 3 approximation). If a point is kept fixed at the center of the image, all spheres -real or virtual- centered around that point will satisfy the linear constraints.




Next: Non-linear approach
Up: Flexible self-calibration
Previous: Flexible self-calibration
Contents
Marc Pollefeys
2000-07-12
![]() :
:
![\begin{displaymath}
\omega^* \sim {\bf KK}^\top \sim
\left[ \begin{array}{ccc} f...
... c_x c_y& f_y^2+c_y^2& c_y \\ c_x & c_y & 1 \end{array}\right]
\end{displaymath}](img661.gif)
![]() . Imposing the rank 3 constraint in this case should be done through the determinant:
. Imposing the rank 3 constraint in this case should be done through the determinant: