Non-linear approach

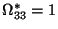Equation (6.7) can be used to obtain the metric calibration from the projective one. The dual image absolute conics $\omega^*_i$ should be parameterized in such a way that they enforce the constraints on the calibration parameters. For the absolute dual quadric $\Omega ^*$ a minimum parameterization (8 parameters) should be used. This can be done by putting $\Omega^*_{33}=1$ and by calculating 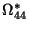$\Omega^*_{44}$ from the rank 3 constraint. The following parameterization satisfies these requirements:

$$\Omega^* = \left[\begin{array}{rr} {\bf KK}^\top & -{\bf KK}... ...p {\bf KK}^\top {\tt\pi}_\infty \end{array}\right] \enspace .$$ (F18)

Here ${\tt\pi}_\infty$ defines the position of the plane at infinity ${\tt\Pi}_\infty=[\,{\tt\pi}_\infty^\top \,1]^\top$. In this case the transformation from projective to metric is particularly simple:

$${\bf T}_{PM} = \left[ \begin{array}{cc} {\bf K}^{-1} & 0_3 \\ {\tt\pi}_\infty^\top & 1\end{array} \right]$$ (F19)

An approximate solution to these equations can be obtained through non-linear least squares. The following criterion should be minimized (with 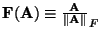${\bf F}({\bf A}) \equiv \frac{\bf A}{\Vert {\bf A}\Vert}_F$ meaning that ${\bf A}$ is normalized to a Frobenius-norm of one):

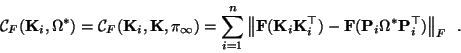$${\cal C}_F({\bf K}_i, \Omega^* ) = {\cal C}_F({\bf K}_i, {\b... ...}({\bf P}_i \Omega^* {\bf P}_i^\top) \right\Vert _F \enspace .$$ (F20)

If one chooses ${\bf P}_1=[{\bf I} \vert {\bf0}]$, equation (6.7) can be rewritten as follows:

$${\bf K}_i{\bf K}_i^\top \sim {\bf P}_i \Omega^*_1 {\bf P}_i^... ...f K}_1 {\bf K}_1^\top {\tt\pi}_\infty^\top \end{array} \right]$$ (F21)

and the following criterion is obtained:

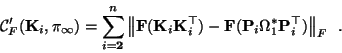$${\cal C}'_F({\bf K}_i, {\tt\pi}_\infty) = \sum_{i={\bf 2}}^{... ...{\bf P}_i \Omega^*_1 {\bf P}_i^\top) \right\Vert _F \enspace .$$ (F22)

In this way 5 of the 8 parameters of the absolute conic are eliminated at once, which simplifies convergence issues. On the other hand this formulation implies a bias towards the first view since using this parameterization the equations for the first view are perfectly satisfied, whereas the noise has to be spread over the equations for the other views. In the experiments it will be seen that this is not suitable for longer sequences where in this case the present redundancy can not be used optimally. Therefore it is proposed to first use the simplified criterion of equation (6.22) and then to refine the results with the unbiased criterion of equation (6.20).

To apply this self-calibration method to standard zooming/focusing cameras, some assumptions should be made. It can safely be assumed that the pixels are rectangular. Often they are squares and for most cameras the principal point can be assumed close to the center of the image. This leads to the following parameterizations for ${\bf K}_i$ (transform the images to have $(0,0)$ in the middle):

$${\bf K}_i= \left[ \begin{array}{ccc} f_i & 0 & c_{xi} \\ & f... ...i & 0 & 0 \\ & f_i & 0 \\ & & 1 \end{array} \right] \enspace .$$ (F23)

These parameterizations can be used in (6.20).