The epipolar constraint restricts the search range for a corresponding
point ![]() in one image to the epipolar line in the other image. It
imposes no restrictions on the object geometry other that the
reconstructed object point
in one image to the epipolar line in the other image. It
imposes no restrictions on the object geometry other that the
reconstructed object point ![]() lays on the line of sight
lays on the line of sight ![]() from
the projection center of
from
the projection center of ![]() and through the corresponding point
and through the corresponding point
![]() as seen in Figure 7.1(left). The search for the
corresponding point
as seen in Figure 7.1(left). The search for the
corresponding point ![]() is restricted to the epipolar line
but no restrictions are imposed along the search line.
is restricted to the epipolar line
but no restrictions are imposed along the search line.
If we now think of the epipolar constraint as being a plane spanned by
the line of sight ![]() and the baseline connecting
the camera projection centers, then we will find the
epipolar line by intersecting the image plane
and the baseline connecting
the camera projection centers, then we will find the
epipolar line by intersecting the image plane ![]() with this
epipolar plane.
with this
epipolar plane.
This plane also intersects the image plane ![]() and it cuts a
3D profile out of the surface of the scene objects. The profile
projects onto the corresponding epipolar lines in
and it cuts a
3D profile out of the surface of the scene objects. The profile
projects onto the corresponding epipolar lines in ![]() and
and
![]() where it forms an ordered set of neighboring
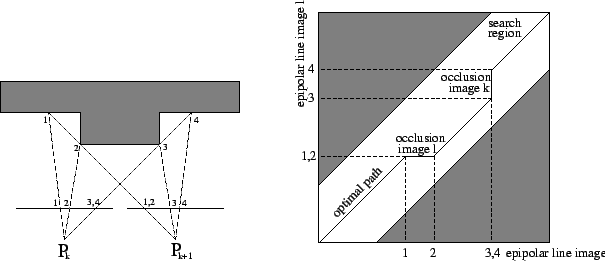
correspondences, as indicated in Figure 7.1 (right).
where it forms an ordered set of neighboring
correspondences, as indicated in Figure 7.1 (right).
For well behaved surfaces this ordering is preserved and delivers an additional constraint, known as 'ordering constraint'. Scene constraints like this can be applied by making weak assumptions about the object geometry. In many real applications the observed objects will be opaque and composed out of piecewise continuous surfaces. If this restriction holds then additional constraints can be imposed on the correspondence estimation. Koschan[92] listed as many as 12 different constraints for correspondence estimation in stereo pairs. Of them, the most important apart from the epipolar constraint are:
 |
All above mentioned constraints operate along the epipolar lines which
may have an arbitrary orientation in the image planes. The matching
procedure is greatly simplified if the image pair is rectified to a
standard geometry. How this can be achieved for an arbitrary image pair
is explained in the Section 7.2.2.
In standard geometry both image planes are coplanar
and the epipoles are projected to infinity. The rectified image planes
are oriented such that the epipolar lines coincide with the
image scan lines. This corresponds to a camera translated in the direction of the ![]() -axis of the image. An example is shown in figure 7.2. In this case the image displacements between the two images or disparities are purely horizontal.
-axis of the image. An example is shown in figure 7.2. In this case the image displacements between the two images or disparities are purely horizontal.