



Next: Tangent to a conic
Up: Conics and quadrics
Previous: Dual conic
Contents
Let 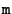 and
and  be two points defining a line. A point on this line can then be represented by
be two points defining a line. A point on this line can then be represented by
 . This point lies on a conic
. This point lies on a conic  if and only if
if and only if
which can also be written as
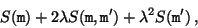 |
(B12) |
where
This means that a line has in general two intersection points with a conic. These intersection points can be real or complex and can be obtained by solving equation (2.12).
Marc Pollefeys
2000-07-12